Question

The sum of all numbers greater than 1000 formed by using the digits 1, 3, 5, 7 such that no digit is be repeated in any number is -

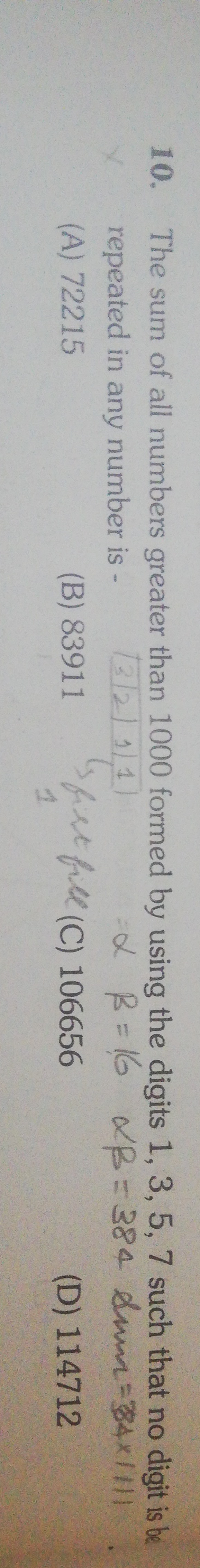
• A. 72215
• B. 83911
• C. 106656
• D. 114712

Answer 1

Answer: (C)

106656

Answer 2

The problem asks for the sum of all 4-digit numbers formed by permuting the digits 1, 3, 5, and 7. There are $4! = 24$ such numbers. Each digit appears $(4-1)! = 6$ times in each place value (thousands, hundreds, tens, ones). The sum is calculated as $(4-1)! \times (\text{sum of digits}) \times 1111 = 6 \times (1+3+5+7) \times 1111 = 6 \times 16 \times 1111 = 96 \times 1111 = 106656$.