Question

The joint equation of bisectors of angles between lines x = 5 and y = 3 is

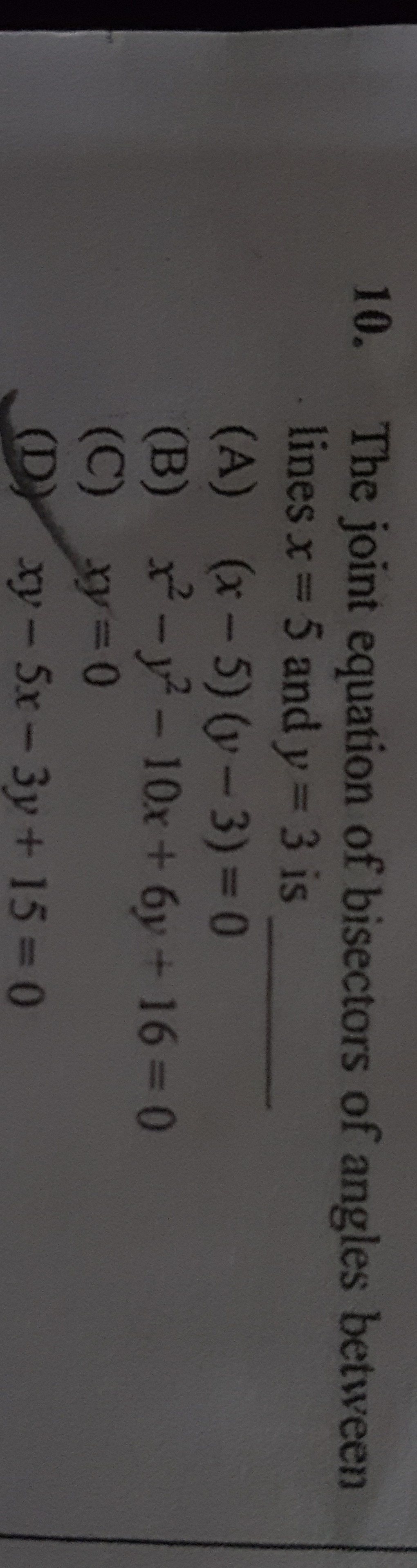
• A. (x-5)(y-3) = 0
• B. $x^2 - y^2 - 10x + 6y + 16 = 0$
• C. xy = 0
• D. xy - 5x - 3y + 15 = 0

Answer 1

Answer: (B)

$x^2 - y^2 - 10x + 6y + 16 = 0$

Answer 2

The given lines are

$x = 5$ and $y = 3$,

which intersect at $(5,3)$. Their angle bisectors satisfy

$y-3 = \pm (x-5)$.

Squaring both equations gives:

$(y-3)^2 = (x-5)^2 \implies (y-3)^2 - (x-5)^2 = 0$.

Expanding:

$y^2 - 6y + 9 - x^2 + 10x - 25 = 0 \implies -x^2 + y^2 + 10x - 6y - 16 = 0$.

Multiplying by $-1$:

$x^2 - y^2 - 10x + 6y + 16 = 0$.