Question

The joint equation of bisectors of angles between lines $x=5$ and $y=3$ is

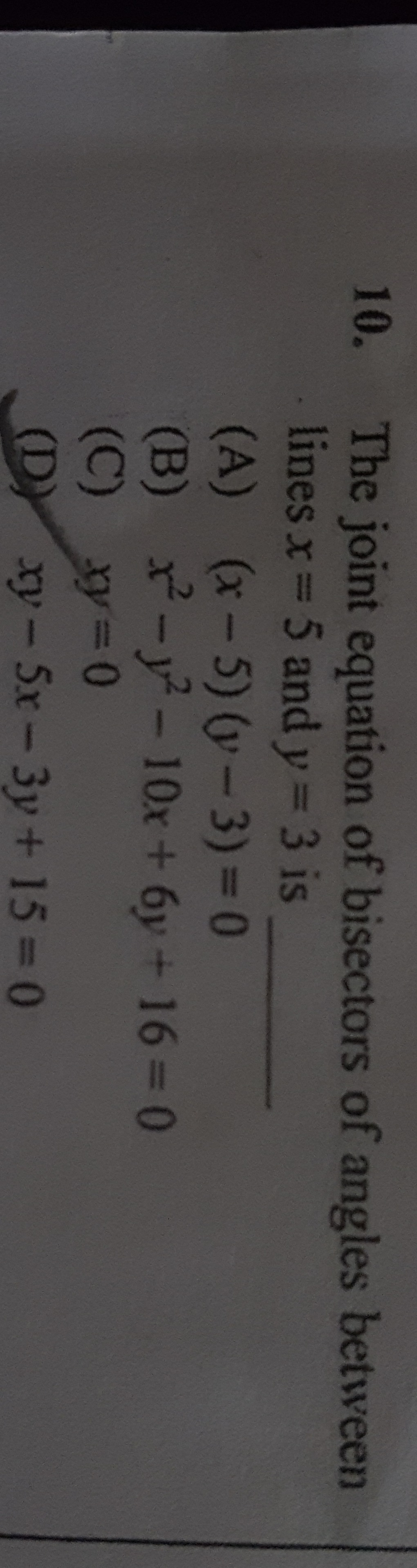
• A. $(x-5)(y-3)=0$
• B. $x^2 - y^2 - 10x + 6y + 16 = 0$
• C. $xy = 0$
• D. $xy - 5x - 3y + 15 = 0$

Answer 1

Answer: (B)

x^2 - y^2 - 10x + 6y + 16 = 0

Answer 2

The given lines are

$x=5$ and $y=3$.

Their intersection is $(5,3)$. The bisectors of the angle between a vertical and a horizontal line are at angles of $45^\circ$ and $135^\circ$.

Thus, the equations of the bisectors passing through $(5,3)$ are:

$y-3 = \pm (x-5)$.

This gives:

$y = x-2,$

$y = -x+8.$

The joint equation is the product:

$(y - (x-2))(y-(-x+8)) = 0 \implies (y-x+2)(y+x-8) = 0$.

Expanding:

$(y-x+2)(y+x-8) = y^2 - x^2 -10x +6y +16 = 0$.

Rearranging, we get:

$x^2 - y^2 -10x +6y +16 = 0$.