Question

Tangent to an ellipse $\frac{x^2}{4} + \frac{y^2}{9} = 1$ makes angles $\theta_1$, $\theta_2$ with positive direction of major axis. Find the locus of their intersection when $cot\theta_1 + cot\theta_2 = k^2$.

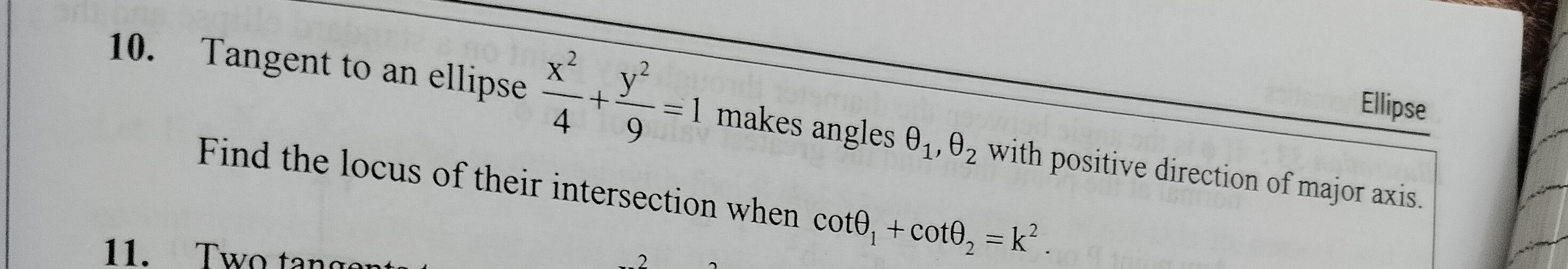
Answer 1

The locus of their intersection is $k^2x^2 - 2xy - 4k^2 = 0$.

Answer 2

The equation of the ellipse is $\frac{x^2}{4} + \frac{y^2}{9} = 1$, with $b^2=4$ and $a^2=9$. The major axis is along the y-axis. The equation of a tangent with slope $m$ is $y = mx \pm \sqrt{4m^2 + 9}$. Rearranging for $m$ gives $m^2(x^2 - 4) - 2mxy + (y^2 - 9) = 0$. If $\theta$ is the angle with the major axis (y-axis), then $m = \cot \theta$. The condition $\cot \theta_1 + \cot \theta_2 = k^2$ becomes $m_1 + m_2 = k^2$. From Vieta's formulas, $m_1 + m_2 = \frac{2xy}{x^2 - 4}$. Equating them gives $\frac{2xy}{x^2 - 4} = k^2$, which simplifies to $k^2x^2 - 2xy - 4k^2 = 0$.