Solveeit Logo
Login

Question

Question: $\lim_{x\to 0}\frac{x+2\sin x}{\sqrt{x^2+2\sin x+1}-\sqrt{\sin^2x-x+1}}$ is:...

lim⁡x→0x+2sin⁡xx2+2sin⁡x+1−sin⁡2x−x+1\lim_{x\to 0}\frac{x+2\sin x}{\sqrt{x^2+2\sin x+1}-\sqrt{\sin^2x-x+1}} is:

A

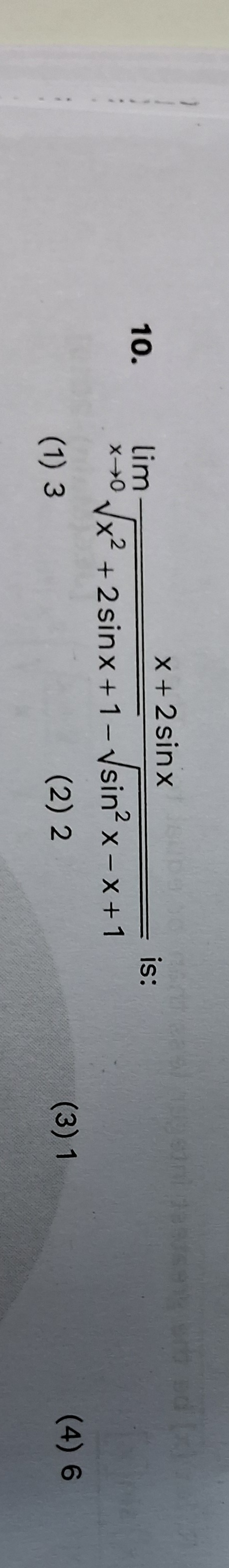
3

B

2

C

1

D

6

Answer

2

Explanation

Solution

To evaluate the limit lim⁡x→0x+2sin⁡xx2+2sin⁡x+1−sin⁡2x−x+1\lim_{x\to 0}\frac{x+2\sin x}{\sqrt{x^2+2\sin x+1}-\sqrt{\sin^2x-x+1}}, we first substitute x=0x=0 into the expression.

Numerator: 0+2sin⁡(0)=00+2\sin(0) = 0.

Denominator: 02+2sin⁡(0)+1−sin⁡2(0)−0+1=1−1=1−1=0\sqrt{0^2+2\sin(0)+1}-\sqrt{\sin^2(0)-0+1} = \sqrt{1}-\sqrt{1} = 1-1 = 0.

Since the limit is of the 00\frac{0}{0} indeterminate form, we can use rationalization or L'Hopital's rule. Rationalization is often effective when square root terms are involved.

Step 1: Rationalize the denominator.

Multiply the numerator and denominator by the conjugate of the denominator, which is x2+2sin⁡x+1+sin⁡2x−x+1\sqrt{x^2+2\sin x+1}+\sqrt{\sin^2x-x+1}.

The expression becomes:

lim⁡x→0(x+2sin⁡x)(x2+2sin⁡x+1+sin⁡2x−x+1)(x2+2sin⁡x+1−sin⁡2x−x+1)(x2+2sin⁡x+1+sin⁡2x−x+1)\lim_{x\to 0}\frac{(x+2\sin x)(\sqrt{x^2+2\sin x+1}+\sqrt{\sin^2x-x+1})}{(\sqrt{x^2+2\sin x+1}-\sqrt{\sin^2x-x+1})(\sqrt{x^2+2\sin x+1}+\sqrt{\sin^2x-x+1})}

Step 2: Simplify the denominator.

Using the difference of squares formula (a−b)(a+b)=a2−b2(a-b)(a+b) = a^2-b^2:

Denominator =(x2+2sin⁡x+1)−(sin⁡2x−x+1)= (x^2+2\sin x+1) - (\sin^2x-x+1) =x2+2sin⁡x+1−sin⁡2x+x−1= x^2+2\sin x+1 - \sin^2x+x-1 =x2−sin⁡2x+2sin⁡x+x= x^2 - \sin^2x + 2\sin x + x

The limit expression is now:

lim⁡x→0(x+2sin⁡x)(x2+2sin⁡x+1+sin⁡2x−x+1)x2−sin⁡2x+2sin⁡x+x\lim_{x\to 0}\frac{(x+2\sin x)(\sqrt{x^2+2\sin x+1}+\sqrt{\sin^2x-x+1})}{x^2 - \sin^2x + 2\sin x + x}

Step 3: Separate the limit into two parts.

(lim⁡x→0x+2sin⁡xx2−sin⁡2x+2sin⁡x+x)×(lim⁡x→0(x2+2sin⁡x+1+sin⁡2x−x+1))\left(\lim_{x\to 0}\frac{x+2\sin x}{x^2 - \sin^2x + 2\sin x + x}\right) \times \left(\lim_{x\to 0}(\sqrt{x^2+2\sin x+1}+\sqrt{\sin^2x-x+1})\right)

Step 4: Evaluate the second part of the limit.

As x→0x \to 0:

lim⁡x→0(x2+2sin⁡x+1+sin⁡2x−x+1)=02+2sin⁡(0)+1+sin⁡2(0)−0+1\lim_{x\to 0}(\sqrt{x^2+2\sin x+1}+\sqrt{\sin^2x-x+1}) = \sqrt{0^2+2\sin(0)+1}+\sqrt{\sin^2(0)-0+1} =0+0+1+0−0+1=1+1=1+1=2= \sqrt{0+0+1}+\sqrt{0-0+1} = \sqrt{1}+\sqrt{1} = 1+1 = 2

Step 5: Evaluate the first part of the limit.

Let L1=lim⁡x→0x+2sin⁡xx2−sin⁡2x+2sin⁡x+xL_1 = \lim_{x\to 0}\frac{x+2\sin x}{x^2 - \sin^2x + 2\sin x + x}.

This is still a 00\frac{0}{0} form. Divide both the numerator and the denominator by xx.

Numerator: x+2sin⁡x=x(1+2sin⁡xx)x+2\sin x = x\left(1+2\frac{\sin x}{x}\right)

Denominator: x2−sin⁡2x+2sin⁡x+x=x(x−sin⁡2xx+2sin⁡xx+1)x^2 - \sin^2x + 2\sin x + x = x\left(x - \frac{\sin^2x}{x} + 2\frac{\sin x}{x} + 1\right)

Note that sin⁡2xx=sin⁡xx⋅sin⁡x\frac{\sin^2x}{x} = \frac{\sin x}{x} \cdot \sin x.

So, L1=lim⁡x→0x(1+2sin⁡xx)x(x−sin⁡xxsin⁡x+2sin⁡xx+1)L_1 = \lim_{x\to 0}\frac{x\left(1+2\frac{\sin x}{x}\right)}{x\left(x - \frac{\sin x}{x}\sin x + 2\frac{\sin x}{x} + 1\right)}

Cancel out xx (since x≠0x \neq 0 as x→0x \to 0):

L1=lim⁡x→01+2sin⁡xxx−sin⁡xxsin⁡x+2sin⁡xx+1L_1 = \lim_{x\to 0}\frac{1+2\frac{\sin x}{x}}{x - \frac{\sin x}{x}\sin x + 2\frac{\sin x}{x} + 1}

Now, apply the standard limit lim⁡x→0sin⁡xx=1\lim_{x\to 0}\frac{\sin x}{x}=1 and lim⁡x→0sin⁡x=0\lim_{x\to 0}\sin x=0.

Numerator: 1+2(1)=31+2(1) = 3.

Denominator: 0−(1)(0)+2(1)+1=0−0+2+1=30 - (1)(0) + 2(1) + 1 = 0 - 0 + 2 + 1 = 3.

So, L1=33=1L_1 = \frac{3}{3} = 1.

Step 6: Combine the results from Step 4 and Step 5.

The original limit is the product of the two parts:

Limit =L1×2=1×2=2= L_1 \times 2 = 1 \times 2 = 2.