Question

$\lim_{x \to 2024} \frac{\tan x - \tan 2024}{\sec x - \sec 2024}$

Answer 1

$\csc 2024$

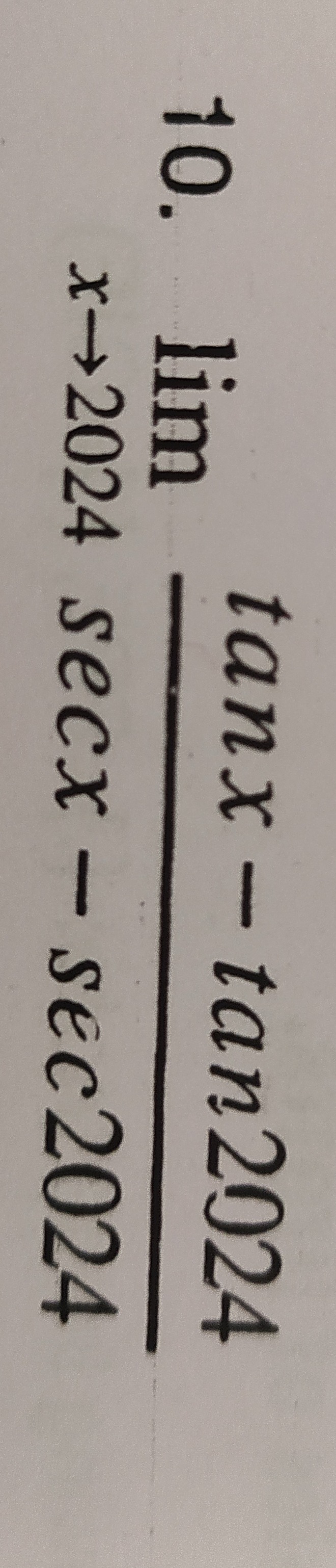
Answer 2

The limit is of the form $\frac{0}{0}$. Using the definition of the derivative, the limit is the ratio of the derivatives of the numerator and denominator functions evaluated at the limit point. The derivative of $\tan x$ is $\sec^2 x$ and the derivative of $\sec x$ is $\sec x \tan x$. Evaluating these at $x = 2024$, we get $\sec^2 2024$ and $\sec 2024 \tan 2024$. The ratio is $\frac{\sec^2 2024}{\sec 2024 \tan 2024} = \frac{\sec 2024}{\tan 2024} = \frac{1/\cos 2024}{\sin 2024/\cos 2024} = \frac{1}{\sin 2024} = \csc 2024$.