Question
Question: $\lim_{x \to 1} \frac{\left(\sum_{k=1}^{100} x^{k}\right)-100}{x-1}$ is equal to...
limx→1x−1(∑k=1100xk)−100 is equal to
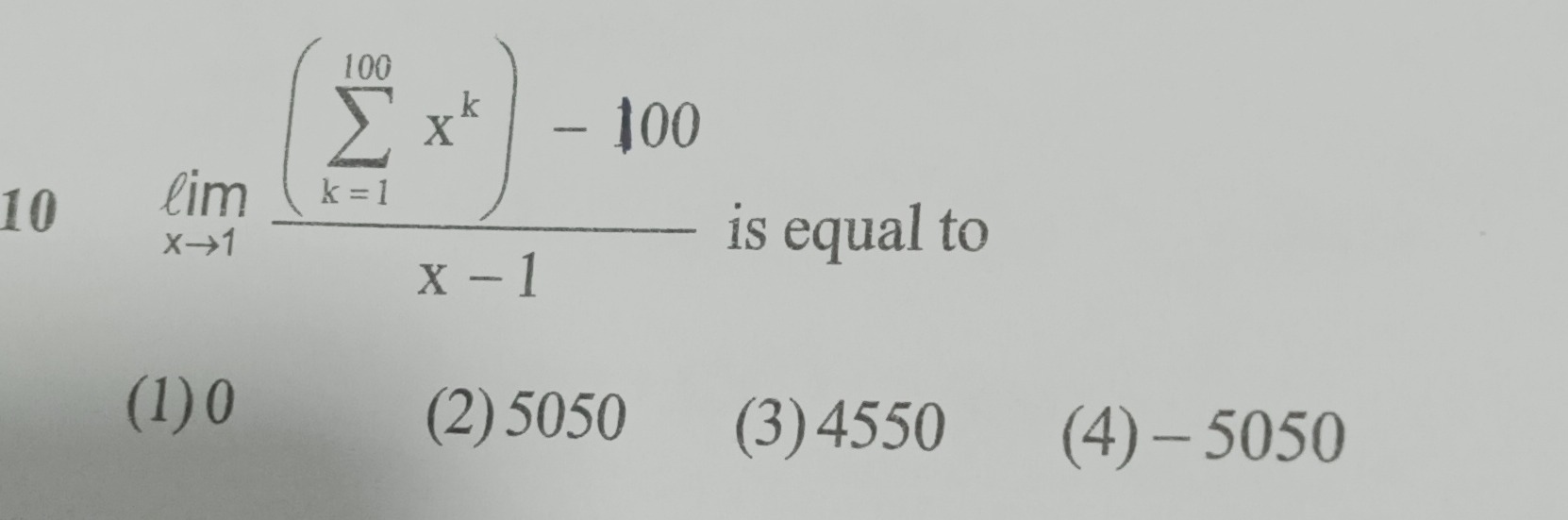
0
5050
4550
-5050
5050
Solution
The given limit is limx→1x−1(∑k=1100xk)−100.
Let f(x)=∑k=1100xk=x+x2+x3+⋯+x100.
We evaluate the numerator and denominator at x=1:
Numerator at x=1: (∑k=11001k)−100=(∑k=11001)−100=100−100=0.
Denominator at x=1: 1−1=0.
Since the limit is of the indeterminate form 00, we can use L'Hôpital's Rule or the definition of the derivative.
Method 1: Using the definition of the derivative.
Let f(x)=∑k=1100xk. Then f(1)=∑k=11001k=100.
The limit can be written as limx→1x−1f(x)−f(1). This is the definition of the derivative of f(x) at x=1, i.e., f′(1).
First, we find the derivative of f(x):
f′(x)=dxd(∑k=1100xk)=dxd(x+x2+⋯+x100).
Using the power rule dxd(xk)=kxk−1, we differentiate each term:
f′(x)=1⋅x1−1+2⋅x2−1+3⋅x3−1+⋯+100⋅x100−1
f′(x)=1+2x+3x2+⋯+100x99.
Now, we evaluate f′(1):
f′(1)=1+2(1)+3(1)2+⋯+100(1)99
f′(1)=1+2+3+⋯+100.
This is the sum of the first 100 positive integers. The sum of the first n positive integers is given by the formula 2n(n+1).
For n=100, the sum is 2100(100+1)=2100×101=50×101=5050.
Therefore, the limit is 5050.
Method 2: Using L'Hôpital's Rule.
Let N(x)=(∑k=1100xk)−100 and D(x)=x−1.
Since limx→1N(x)=0 and limx→1D(x)=0, we can apply L'Hôpital's Rule:
limx→1D(x)N(x)=limx→1D′(x)N′(x).
N′(x)=dxd(∑k=1100xk−100)=dxd(∑k=1100xk)−dxd(100)
N′(x)=∑k=1100dxd(xk)−0=∑k=1100kxk−1=1+2x+3x2+⋯+100x99.
D′(x)=dxd(x−1)=1.
So, the limit is limx→111+2x+3x2+⋯+100x99.
Substituting x=1:
1+2(1)+3(1)2+⋯+100(1)99=1+2+3+⋯+100.
This is the sum of the first 100 positive integers, which is 2100(100+1)=5050.
Both methods give the same result.
