Question

Let's consider two statements. $S_1$ : 3cosx-4 sin x=5 sin($\theta$-x), where tan $\theta$ = $\frac{4}{3}$ $S_2$:3 cos x-4 sin x = 5 cos($\theta$+ x), where tan $\theta$ = $\frac{3}{4}$

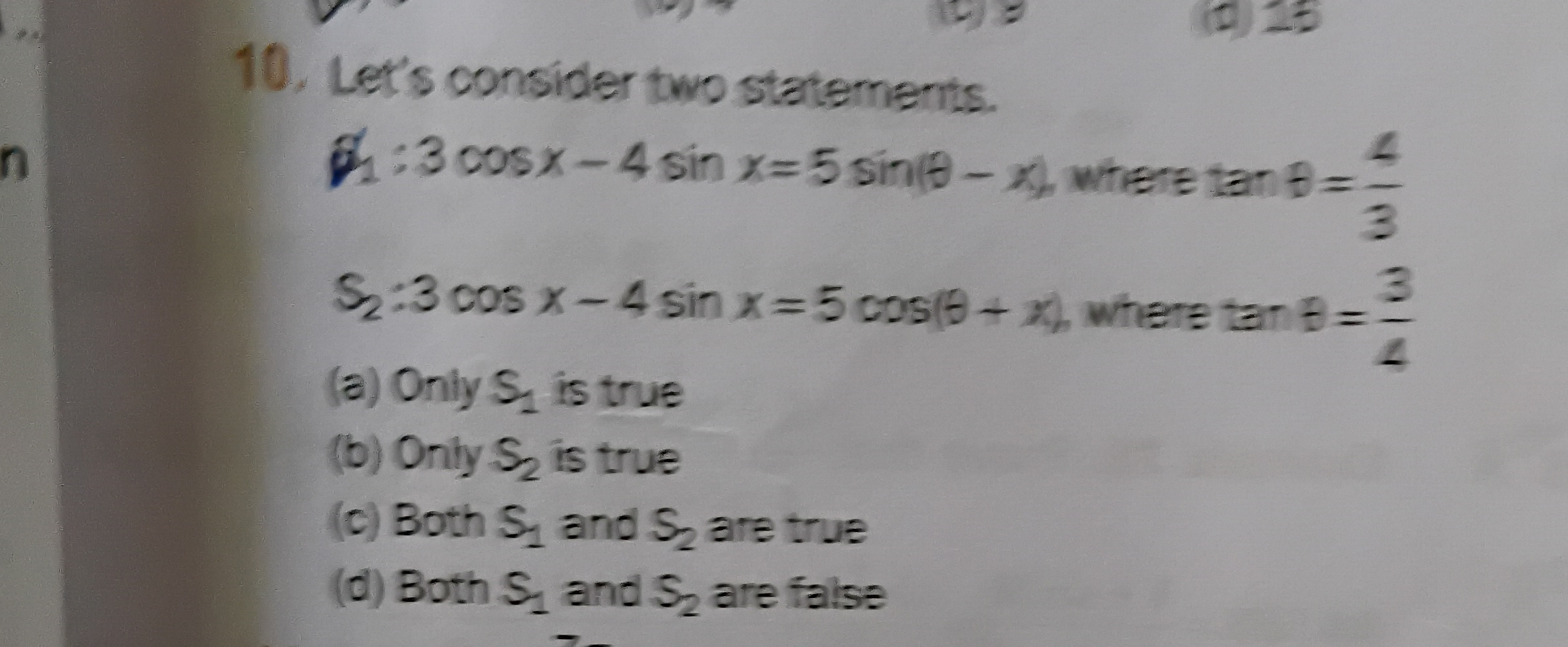
• A. Only $S_1$ is true
• B. Only $S_2$ is true
• C. Both $S_1$ and $S_2$ are true
• D. Both $S_1$ and $S_2$ are false

Answer 1

Answer: (D)

Both $S_1$ and $S_2$ are false

Answer 2

We analyze each statement separately.

Statement $S_1$: $3\cos x - 4\sin x = 5\sin(\theta - x)$, where $\tan \theta = \frac{4}{3}$.

We can express $a\cos x + b\sin x$ in the form $R\sin(\phi - x)$. Let $3\cos x - 4\sin x = R\sin(\phi - x)$. Expanding $R\sin(\phi - x) = R(\sin\phi\cos x - \cos\phi\sin x)$. Comparing coefficients with $3\cos x - 4\sin x$: $R\sin\phi = 3$ $R\cos\phi = 4$

Squaring and adding these equations gives $R^2(\sin^2\phi + \cos^2\phi) = 3^2 + 4^2$, so $R^2 = 25$, and $R=5$ (taking $R>0$). From $R\sin\phi = 3$ and $R\cos\phi = 4$, we get $\tan\phi = \frac{R\sin\phi}{R\cos\phi} = \frac{3}{4}$. Thus, $3\cos x - 4\sin x = 5\sin(\phi - x)$ where $\tan\phi = \frac{3}{4}$.

Statement $S_1$ claims $3\cos x - 4\sin x = 5\sin(\theta - x)$ where $\tan \theta = \frac{4}{3}$. For $S_1$ to be true, we would need $5\sin(\phi - x) = 5\sin(\theta - x)$ for all $x$, with $\tan\phi = 3/4$ and $\tan\theta = 4/3$. This implies $\phi = \theta + n\pi$ for some integer $n$. However, if $\tan\phi = 3/4$ and $\tan\theta = 4/3$, then $\phi \neq \theta + n\pi$. Therefore, $S_1$ is false.

Statement $S_2$: $3\cos x - 4\sin x = 5\cos(\theta + x)$, where $\tan \theta = \frac{3}{4}$.

Let $3\cos x - 4\sin x = R\cos(\phi + x)$. Expanding $R\cos(\phi + x) = R(\cos\phi\cos x - \sin\phi\sin x)$. Comparing coefficients with $3\cos x - 4\sin x$: $R\cos\phi = 3$ $R\sin\phi = 4$

Again, $R=5$. From $R\cos\phi = 3$ and $R\sin\phi = 4$, we get $\tan\phi = \frac{R\sin\phi}{R\cos\phi} = \frac{4}{3}$. Thus, $3\cos x - 4\sin x = 5\cos(\phi + x)$ where $\tan\phi = \frac{4}{3}$.

Statement $S_2$ claims $3\cos x - 4\sin x = 5\cos(\theta + x)$ where $\tan \theta = \frac{3}{4}$. For $S_2$ to be true, we would need $5\cos(\phi + x) = 5\cos(\theta + x)$ for all $x$, with $\tan\phi = 4/3$ and $\tan\theta = 3/4$. This implies $\phi + x = \pm (\theta + x) + 2k\pi$. If $\phi + x = \theta + x + 2k\pi$, then $\phi = \theta + 2k\pi$, which implies $\tan\phi = \tan\theta$. This is not true as $4/3 \neq 3/4$. If $\phi + x = -(\theta + x) + 2k\pi$, then $2x = -\phi - \theta + 2k\pi$, which is not true for all $x$. Therefore, $S_2$ is false.

Since both $S_1$ and $S_2$ are false, the correct option is (d).