Question

Let g(x) =

$\begin{cases} 2x + \tan^{-1}x + a, -\infty < x \leq 0 \\ x^3+x^2+bx, \quad 0 < x < \infty \end{cases}$

If g(x) is differentiable for all $x \in (-\infty, \infty)$, then ($a^2 + b^2$) is equal to:

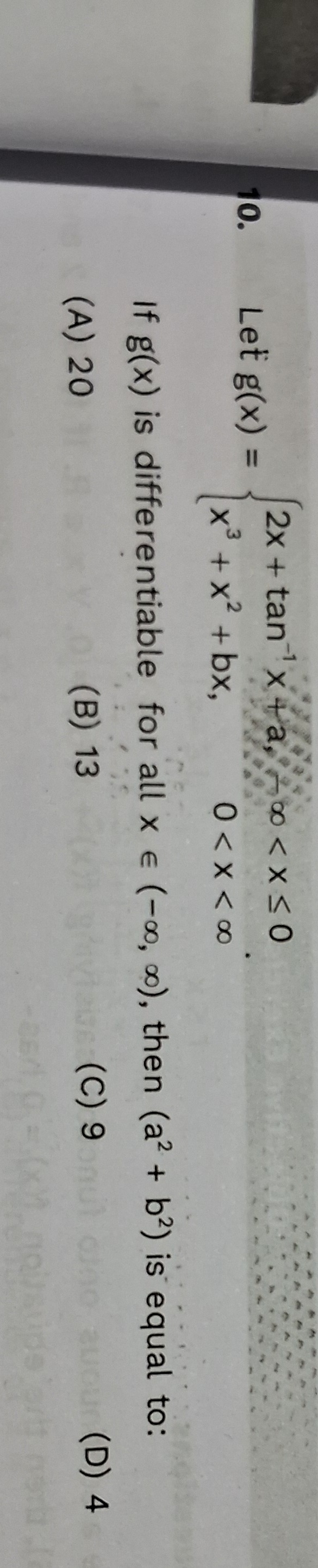
• A. 20
• B. 13
• C. 9
• D. 4

Answer 1

Answer: (C)

9

Answer 2

To ensure that $g(x)$ is differentiable for all $x \in (-\infty, \infty)$, it must satisfy two conditions at $x=0$:

1. Continuity at $x=0$.
2. Differentiability at $x=0$.

Step 1: Ensure continuity at $x=0$

For $g(x)$ to be continuous at $x=0$, we must have $\lim_{x \to 0^-} g(x) = \lim_{x \to 0^+} g(x) = g(0)$.

Left-hand limit: $\lim_{x \to 0^-} g(x) = \lim_{x \to 0^-} (2x + \tan^{-1}x + a) = 2(0) + \tan^{-1}(0) + a = 0 + 0 + a = a$.

Right-hand limit: $\lim_{x \to 0^+} g(x) = \lim_{x \to 0^+} (x^3+x^2+bx) = (0)^3+(0)^2+b(0) = 0 + 0 + 0 = 0$.

Value of the function at $x=0$: $g(0) = 2(0) + \tan^{-1}(0) + a = a$.

For continuity, these values must be equal: $a = 0$.

Step 2: Ensure differentiability at $x=0$

For $g(x)$ to be differentiable at $x=0$, the left-hand derivative (LHD) must be equal to the right-hand derivative (RHD).

First, find the derivative of each piece of the function: For $x < 0$, $g(x) = 2x + \tan^{-1}x + a$. $g'(x) = \frac{d}{dx}(2x + \tan^{-1}x + a) = 2 + \frac{1}{1+x^2}$.

For $x > 0$, $g(x) = x^3+x^2+bx$. $g'(x) = \frac{d}{dx}(x^3+x^2+bx) = 3x^2 + 2x + b$.

Now, calculate the LHD and RHD at $x=0$: Left-hand derivative at $x=0$: $LHD = \lim_{x \to 0^-} g'(x) = 2 + \frac{1}{1+(0)^2} = 2 + 1 = 3$.

Right-hand derivative at $x=0$: $RHD = \lim_{x \to 0^+} g'(x) = 3(0)^2 + 2(0) + b = 0 + 0 + b = b$.

For differentiability, LHD = RHD: $3 = b$.

Step 3: Calculate $a^2 + b^2$

From Step 1, we found $a = 0$. From Step 2, we found $b = 3$.

Now, substitute these values into the expression $a^2 + b^2$: $a^2 + b^2 = (0)^2 + (3)^2 = 0 + 9 = 9$.