Solveeit Logo
Login

Question

Question: In an octagon ABCDEFGH of equal side, what is the sum of $\overline{AB}+\overline{AC}+\overline{AD}+...

In an octagon ABCDEFGH of equal side, what is the sum of AB‾+AC‾+AD‾+AE‾+AF‾+AG‾+AH‾\overline{AB}+\overline{AC}+\overline{AD}+\overline{AE}+\overline{AF}+\overline{AG}+\overline{AH} if, AO‾=2i^+3j^−4k^\overline{AO}=2\hat{i}+3\hat{j}-4\hat{k} ?

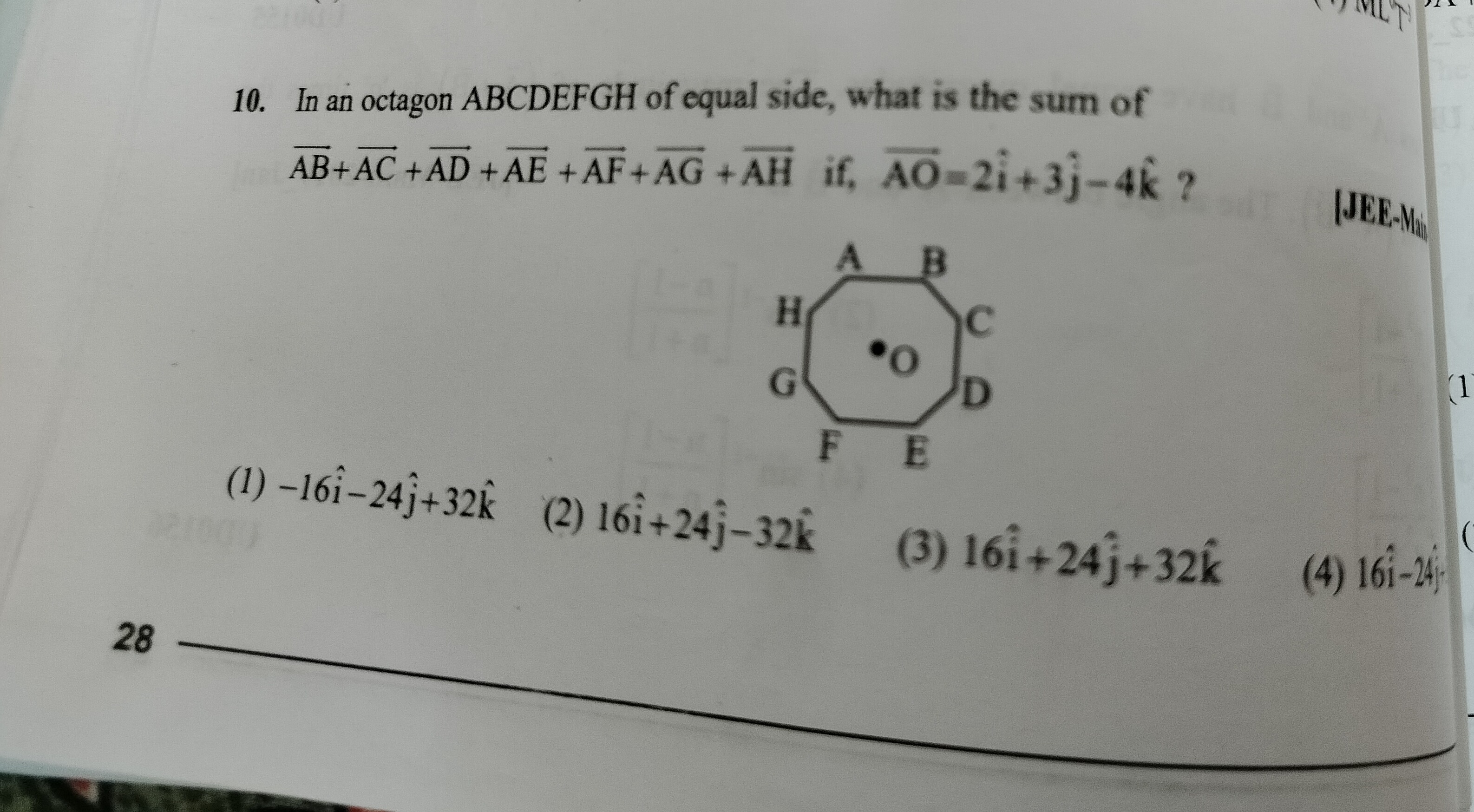
A

−16i^−24j^+32k^-16\hat{i}-24\hat{j}+32\hat{k}

B

16i^+24j^−32k^16\hat{i}+24\hat{j}-32\hat{k}

C

16i^+24j^+32k^16\hat{i}+24\hat{j}+32\hat{k}

D

16i^−24j^16\hat{i}-24\hat{j}

Answer

16i^+24j^−32k^16\hat{i}+24\hat{j}-32\hat{k}

Explanation

Solution

Let O be the center of the regular octagon. The sum of vectors from the center to the vertices is zero: ∑i=AHOi‾=0⃗\sum_{i=A}^H \overline{Oi} = \vec{0}.

The sum of vectors from vertex A to other vertices is S=∑i=BHAi‾S = \sum_{i=B}^H \overline{Ai}.

We can write Ai‾=Oi‾−OA‾\overline{Ai} = \overline{Oi} - \overline{OA}.

S=∑i=BH(Oi‾−OA‾)=∑i=BHOi‾−∑i=BHOA‾=∑i=BHOi‾−7OA‾S = \sum_{i=B}^H (\overline{Oi} - \overline{OA}) = \sum_{i=B}^H \overline{Oi} - \sum_{i=B}^H \overline{OA} = \sum_{i=B}^H \overline{Oi} - 7\overline{OA}.

From ∑i=AHOi‾=0⃗\sum_{i=A}^H \overline{Oi} = \vec{0}, we have OA‾+∑i=BHOi‾=0⃗\overline{OA} + \sum_{i=B}^H \overline{Oi} = \vec{0}, so ∑i=BHOi‾=−OA‾\sum_{i=B}^H \overline{Oi} = -\overline{OA}.

Substituting this into the expression for S: S=−OA‾−7OA‾=−8OA‾S = -\overline{OA} - 7\overline{OA} = -8\overline{OA}.

We are given AO‾=2i^+3j^−4k^\overline{AO} = 2\hat{i}+3\hat{j}-4\hat{k}.

OA‾=−AO‾=−(2i^+3j^−4k^)=−2i^−3j^+4k^\overline{OA} = -\overline{AO} = -(2\hat{i}+3\hat{j}-4\hat{k}) = -2\hat{i}-3\hat{j}+4\hat{k}.

S=−8(−2i^−3j^+4k^)=16i^+24j^−32k^S = -8(-2\hat{i}-3\hat{j}+4\hat{k}) = 16\hat{i}+24\hat{j}-32\hat{k}.

Answer: 16i^+24j^−32k^16\hat{i}+24\hat{j}-32\hat{k}