Question
Question: If $y = \sec^{-1}(\frac{x+x^{-1}}{x-x^{-1}})$, then $\frac{dy}{dx} = $...
If y=sec−1(x−x−1x+x−1), then dxdy=
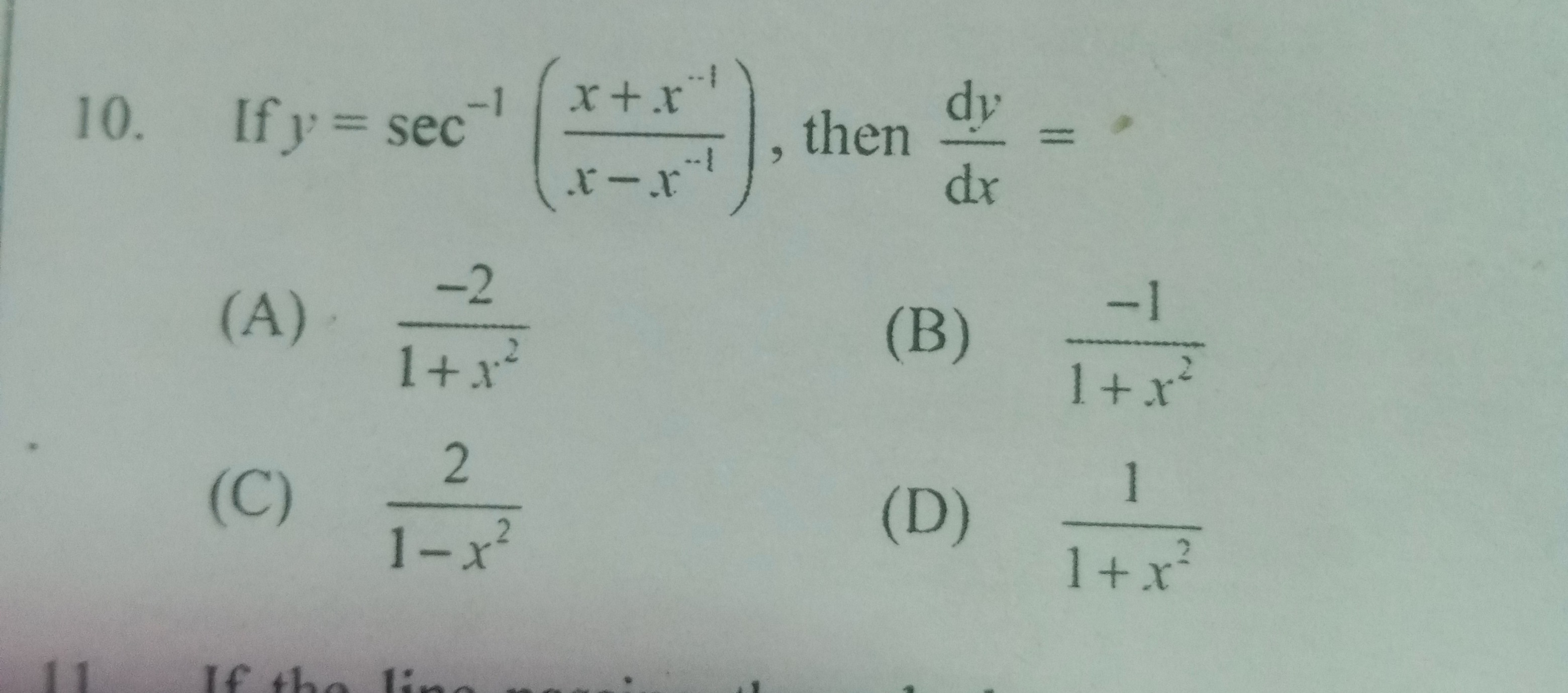
1+x2−2
1+x2−1
1−x22
1+x21
1+x2−2
Solution
The given function is y=sec−1(x−x−1x+x−1).
First, simplify the argument of the sec−1 function:
x−x−1x+x−1=x−x1x+x1=xx2−1xx2+1=x2−1x2+1.
So, y=sec−1(x2−1x2+1).
We can use the identity sec−1(u)=cos−1(u1) for ∣u∣≥1.
The argument is u=x2−1x2+1. For the function to be defined, we must have ∣u∣≥1, i.e., x2−1x2+1≥1.
Since x2+1>0, this is equivalent to ∣x2−1∣x2+1≥1, which means x2+1≥∣x2−1∣.
If x2−1>0, i.e., ∣x∣>1, then x2+1≥x2−1, which is true (1≥−1).
If x2−1<0, i.e., ∣x∣<1 and x=0, then x2+1≥−(x2−1)=1−x2, which means 2x2≥0, which is true for x=0.
The function is defined for x∈R∖{−1,0,1}.
Case 1: ∣x∣>1.
In this case, x2−1>0, and x2−1x2+1>1.
y=sec−1(x2−1x2+1)=cos−1(x2+1x2−1).
Let x=cotθ. Since ∣x∣>1, we have 0<θ<4π (if x>1) or 43π<θ<π (if x<−1).
x2+1x2−1=cot2θ+1cot2θ−1=sin2θcos2θ+1sin2θcos2θ−1=cos2θ+sin2θcos2θ−sin2θ=cos(2θ).
So, y=cos−1(cos(2θ)).
If x>1, then 0<θ<4π, so 0<2θ<2π. In this range, cos−1(cos(2θ))=2θ.
y=2θ=2cot−1(x).
dxdy=2⋅1+x2−1=1+x2−2.
If x<−1, then 43π<θ<π, so 23π<2θ<2π.
In this range, cos(2θ)=cos(2π−2θ). Also, 0<2π−2θ<2π.
So cos−1(cos(2θ))=cos−1(cos(2π−2θ))=2π−2θ.
y=2π−2θ=2π−2cot−1(x).
dxdy=0−2⋅1+x2−1=1+x22.
The derivative depends on whether x>1 or x<−1. However, the options are single expressions. Let's check the other case.
Case 2: ∣x∣<1 and x=0.
In this case, x2−1<0, and x2−1x2+1<−1.
y=sec−1(x2−1x2+1).
Let x=tanθ. Since ∣x∣<1,x=0, we have −4π<θ<4π, θ=0.
x2−1x2+1=tan2θ−1tan2θ+1=−(1−tan2θ)1+tan2θ=−cos(2θ)/cos2θsec2θ=−cos(2θ)/cos2θ1/cos2θ=−cos(2θ)1=−sec(2θ).
So, y=sec−1(−sec(2θ)).
If −4π<θ<4π,θ=0, then −2π<2θ<2π,2θ=0.
In this range, cos(2θ)>0, so sec(2θ)>0.
Let v=−sec(2θ). Then v<0.
We need to evaluate sec−1(v) where v<−1.
Let v=−sec(2θ). Since sec−1(−u)=π−sec−1(u) for u≥1.
y=sec−1(−sec(2θ)). Here u=sec(2θ)=cos(2θ)1.
Since −2π<2θ<2π,2θ=0, we have cos(2θ)>0.
If 0<∣x∣<1, then 0<x2<1, so −1<x2−1<0. x2+1>1.
x2−1x2+1<−1.
So −sec(2θ)<−1, which means sec(2θ)>1. This is true since 0<∣2θ∣<2π.
y=π−sec−1(sec(2θ)).
Since 0<∣2θ∣<2π, we have 2θ∈(−2π,0)∪(0,2π).
If 0<2θ<2π (i.e., 0<θ<4π, which means 0<x<1), then sec−1(sec(2θ))=2θ.
y=π−2θ=π−2tan−1(x).
dxdy=0−2⋅1+x21=1+x2−2.
If −2π<2θ<0 (i.e., −4π<θ<0, which means −1<x<0), then sec−1(sec(2θ))=−2θ.
y=π−(−2θ)=π+2θ=π+2tan−1(x).
dxdy=0+2⋅1+x21=1+x22.
The derivative is 1+x2−2 for ∣x∣>1 and for 0<x<1.
The derivative is 1+x22 for −1<x<0.
Let's look at the options again. Option (A) is 1+x2−2. This matches the derivative for x∈(0,1)∪(∣x∣>1).
Option (D) is 1+x21.
Option (B) is 1+x2−1.
Option (C) is 1−x22.
It seems there might be a domain restriction implied or a standard convention used in the problem. Often in such problems, the principal values are considered, and the domain is chosen such that the simplification holds directly.
Let's re-examine the substitution x=cotθ.
y=sec−1(sec(2θ)).
The principal range of sec−1(u) is [0,π]−{2π}.
We need 2θ to be in this range.
If x>0, then 0<θ<2π. So 0<2θ<π.
If 2θ=2π, i.e., θ=4π, i.e., x=cot(4π)=1.
For x>0,x=1, we have 2θ∈(0,π)−{2π}.
In this range, sec−1(sec(2θ))=2θ.
So for x>0,x=1, y=2θ=2cot−1(x).
dxdy=2⋅1+x2−1=1+x2−2.
If x<0, then 2π<θ<π. So π<2θ<2π.
We need to express sec(2θ) as sec(ϕ) where ϕ∈[0,π]−{2π}.
Let ϕ=2π−2θ. Then 0<ϕ<π.
sec(ϕ)=sec(2π−2θ)=sec(2θ).
So y=sec−1(sec(2θ))=sec−1(sec(2π−2θ)).
If 2π−2θ∈[0,π]−{2π}, then y=2π−2θ.
2π−2θ=2π implies 2θ=23π, θ=43π, x=cot(43π)=−1. The function is undefined at x=−1.
For x<0,x=−1, we have 2π<θ<π,θ=43π.
So π<2θ<2π,2θ=23π.
0<2π−2θ<π,2π−2θ=2π.
So 2π−2θ∈(0,π)−{2π}.
Thus, for x<0,x=−1, y=2π−2θ=2π−2cot−1(x).
dxdy=0−2⋅1+x2−1=1+x22.
The derivative is 1+x2−2 for x>0,x=1.
The derivative is 1+x22 for x<0,x=−1.
Let's consider the substitution x=tanθ.
y=sec−1(−sec(2θ)).
Principal range of sec−1 is [0,π]−{2π}.
If 0<x<1, then 0<θ<4π, so 0<2θ<2π. sec(2θ)>1. −sec(2θ)<−1.
Let u=sec(2θ). y=sec−1(−u)=π−sec−1(u)=π−sec−1(sec(2θ))=π−2θ=π−2tan−1(x).
dxdy=0−2⋅1+x21=1+x2−2.
If x>1, then 4π<θ<2π, so 2π<2θ<π. sec(2θ)<−1.
y=sec−1(−sec(2θ)). Let v=−sec(2θ). v>1.
Let ϕ=2θ−π. Then −2π<ϕ<0. sec(ϕ)=sec(2θ−π)=sec(π−2θ)=−sec(2θ).
So y=sec−1(sec(ϕ)). Since −2π<ϕ<0, sec(ϕ)>1.
y=sec−1(sec(ϕ))=−ϕ=−(2θ−π)=π−2θ=π−2tan−1(x).
dxdy=1+x2−2.
If −1<x<0, then −4π<θ<0, so −2π<2θ<0. sec(2θ)>1. −sec(2θ)<−1.
y=sec−1(−sec(2θ)). Let u=sec(2θ). y=π−sec−1(u)=π−sec−1(sec(2θ))=π−(−2θ)=π+2θ=π+2tan−1(x).
dxdy=0+2⋅1+x21=1+x22.
If x<−1, then −2π<θ<−4π, so −π<2θ<−2π. sec(2θ)<−1.
y=sec−1(−sec(2θ)). Let v=−sec(2θ). v>1.
Let ϕ=2θ+π. Then 2π<ϕ<π. sec(ϕ)=sec(2θ+π)=−sec(2θ).
y=sec−1(sec(ϕ)). Since 2π<ϕ<π, sec(ϕ)<−1.
y=ϕ=2θ+π=2tan−1(x)+π.
dxdy=2⋅1+x21=1+x22.
Summary of derivatives:
If x∈(0,1)∪(1,∞), dxdy=1+x2−2.
If x∈(−∞,−1)∪(−1,0), dxdy=1+x22.
Since option (A) 1+x2−2 is given, it is likely that the domain considered in the question is x>0. In many standard problems involving inverse trigonometric functions, a specific domain is implicitly assumed to get a single answer. If the question is from a single-choice context, and option (A) is the intended answer, the domain x>0 is implied.
Let's verify if there is any property that leads to a single derivative.
Consider y=cos−1(x2+1x2−1).
Let x2=t. y=cos−1(t+1t−1).
Let t+1t−1=−cosα.
1+t1−t=cosα.
If t=tan2β, 1+tan2β1−tan2β=cos(2β).
So x2+1x2−1=−cos(2β).
y=cos−1(−cos(2β))=π−cos−1(cos(2β)).
If x>0, let x=tanθ, x2=tan2θ. Let β=θ.
y=π−cos−1(cos(2θ)).
If x>0, 0<θ<2π. 0<2θ<π.
If 0<2θ<π, cos−1(cos(2θ))=2θ.
y=π−2θ=π−2tan−1(x).
dxdy=−21+x21. This is valid for x>0.
If x<0, let x=−tanϕ, where ϕ>0.
x2=tan2ϕ.
y=cos−1(cos(2ϕ)).
If x<0, x=−tanϕ. We need to relate ϕ to x. ϕ=tan−1(−x).
y=cos−1(cos(2tan−1(−x))).
If x<0, let x=−a where a>0. y=cos−1(a2+1a2−1).
Let a=cotθ, 0<θ<2π.
y=cos−1(cos(2θ)). 0<2θ<π.
y=2θ=2cot−1(a)=2cot−1(−x).
dxdy=2⋅1+(−x)2−1⋅(−1)=1+x22.
The derivative is 1+x2−2 for x>0 and 1+x22 for x<0.
The options suggest a single answer. Option (A) is 1+x2−2. This is the result when x>0.
Let's check if the question implies a specific domain. The form x−x−1x+x−1 suggests x=0. The term x−x−1 in the denominator suggests x=±1.
The domain of sec−1(u) is ∣u∣≥1. We found that this is true for all x∈R∖{−1,0,1}.
Consider the derivative of sec−1(u) is ∣u∣u2−11.
If we are required to choose one option, and option (A) appears as a valid derivative for a significant part of the domain (x>0), it is likely the intended answer.
Let's check the derivative formula for sec−1(u) again.
dud(sec−1u)=∣u∣u2−11.
u=x2−1x2+1. dxdu=(x2−1)2−4x.
u2−1=∣x2−1∣2∣x∣.
dxdy=x2−1x2+1∣x2−1∣2∣x∣1⋅(x2−1)2−4x=(x2+1)2∣x∣∣x2−1∣2(x2−1)2−4x=(x2+1)2∣x∣(x2−1)2(x2−1)2−4x=(x2+1)2∣x∣−4x=(x2+1)∣x∣−2x.
If x>0, ∣x∣=x, dxdy=(x2+1)x−2x=x2+1−2.
If x<0, ∣x∣=−x, dxdy=(x2+1)(−x)−2x=x2+12.
The derivative is 1+x2−2 for x>0 and 1+x22 for x<0.
Assuming the question implicitly considers the domain x>0 (as is common when a single option is correct), the derivative is 1+x2−2.
