Question
Question: If $x^4 + 3\cos(ax^2+bx+c) = 2(x^2-2)$ has two solutions with a,b,c $\in$ (2,5) then...
If x4+3cos(ax2+bx+c)=2(x2−2) has two solutions with a,b,c ∈ (2,5) then
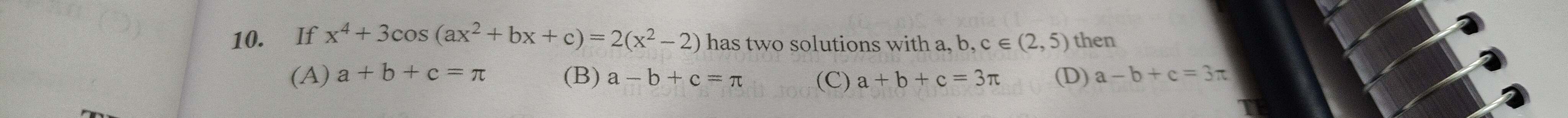
a + b + c = π
a - b + c = π
a + b + c = 3π
a - b + c = 3π
C
Solution
The given equation is x4+3cos(ax2+bx+c)=2(x2−2). Rearranging the terms, we get x4−2x2+4+3cos(ax2+bx+c)=0.
We can rewrite the term x4−2x2+4 as follows: x4−2x2+1+3=(x2−1)2+3.
Substitute this back into the equation: (x2−1)2+3+3cos(ax2+bx+c)=0, which can be written as (x2−1)2+3(1+cos(ax2+bx+c))=0.
We know the following properties:
- (x2−1)2≥0 for any real x.
- The range of cos(θ) is [−1,1]. Therefore, 1+cos(θ)≥1+(−1)=0. So, 3(1+cos(ax2+bx+c))≥0.
The sum of two non-negative terms is zero if and only if both terms are individually zero. Therefore, we must have:
- (x2−1)2=0
- 3(1+cos(ax2+bx+c))=0
From condition (1): (x2−1)2=0⟹x2−1=0⟹x2=1⟹x=±1. These are the two solutions mentioned in the problem statement.
From condition (2): 1+cos(ax2+bx+c)=0⟹cos(ax2+bx+c)=−1. This condition must hold for both solutions x=1 and x=−1.
Case 1: For x=1
Substitute x=1 into the argument of cosine: cos(a(1)2+b(1)+c)=−1, so cos(a+b+c)=−1. For cos(θ)=−1, θ must be an odd multiple of π. So, a+b+c=(2n+1)π for some integer n.
We are given that a,b,c∈(2,5). Let's find the range of a+b+c: 2<a<5, 2<b<5, 2<c<5. Adding these inequalities: 2+2+2<a+b+c<5+5+5⟹6<a+b+c<15.
Now, let's check which odd multiple of π falls into this range:
If n=0, a+b+c=π≈3.14 (not in (6,15)).
If n=1, a+b+c=3π≈9.42 (is in (6,15)).
If n=2, a+b+c=5π≈15.70 (not in (6,15)).
Thus, for x=1, we must have a+b+c=3π. This matches option (C).
Case 2: For x=−1
Substitute x=−1 into the argument of cosine: cos(a(−1)2+b(−1)+c)=−1, so cos(a−b+c)=−1. Similarly, a−b+c=(2m+1)π for some integer m.
Let's find the range of a−b+c: 2<a<5, −5<−b<−2 (multiplying 2<b<5 by -1 and reversing inequalities), 2<c<5. Adding these inequalities: 2+(−5)+2<a−b+c<5+(−2)+5⟹−1<a−b+c<8.
Now, let's check which odd multiple of π falls into this range:
If m=−1, a−b+c=−π≈−3.14 (not in (−1,8)).
If m=0, a−b+c=π≈3.14 (is in (−1,8)).
If m=1, a−b+c=3π≈9.42 (not in (−1,8)).
Thus, for x=−1, we must have a−b+c=π. This matches option (B).
Both conditions, a+b+c=3π and a−b+c=π, must be true simultaneously for the equation to hold for x=±1 under the given constraints on a,b,c.
We can check for consistency:
Adding the two derived equations: (a+b+c)+(a−b+c)=3π+π⟹2a+2c=4π⟹a+c=2π.
Since a,c∈(2,5), a+c∈(4,10). 2π≈6.28 which is indeed in (4,10).
Subtracting the second equation from the first: (a+b+c)−(a−b+c)=3π−π⟹2b=2π⟹b=π.
Since b∈(2,5), π≈3.14 which is indeed in (2,5).
All conditions are consistent.
Since both options (B) and (C) are necessarily true based on the problem statement, and assuming this is a single-choice question, there might be an issue with the question itself. However, if forced to select one, we present one of the derived correct statements.
