Question

If the p.m.f. of r.v. x is

$$P(x=x) = \frac{1}{10} \text{ for } x=1, 2, ........ 10$$ $$= 0 \text{ otherwise,}$$

Then Var(x) is equal to

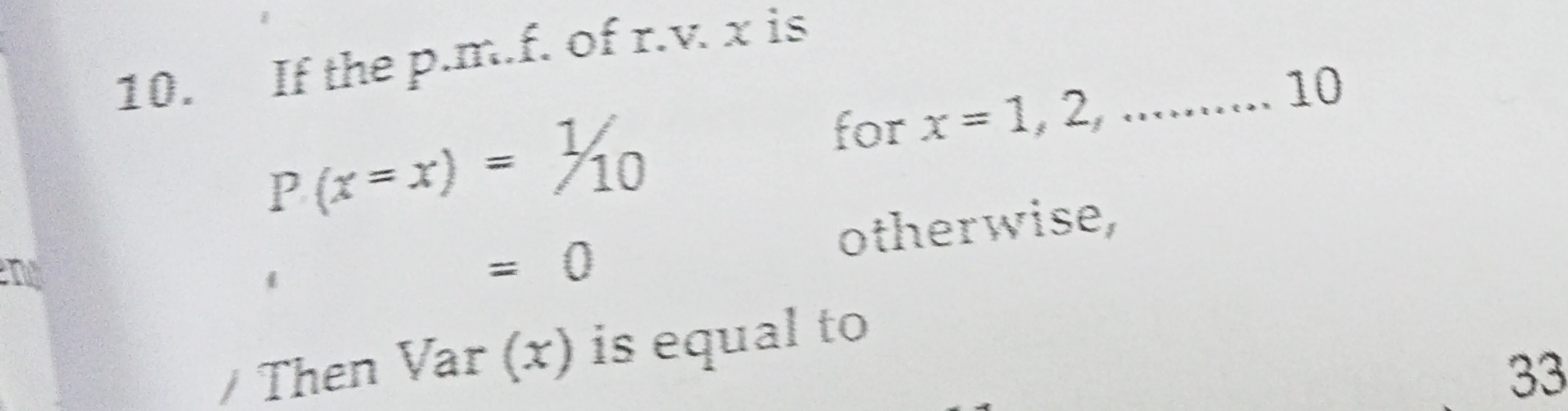
Answer 1

8.25

Answer 2

To find the variance Var(x), we first calculate the expected value E[X] and E[X^2].

1. Calculate the Mean (E[X]):

   $$E[X] = \sum_{x=1}^{10} x \cdot \frac{1}{10} = \frac{1}{10}(1+2+\cdots+10) = \frac{55}{10} = 5.5$$

2. Calculate E[X²]:

   $$E[X^2] = \sum_{x=1}^{10} x^2 \cdot \frac{1}{10} = \frac{1}{10}(1^2 + 2^2 + \cdots + 10^2) = \frac{385}{10} = 38.5$$

   (Note: $\sum_{x=1}^{10} x^2 = \frac{10 \times 11 \times 21}{6} = 385$)

3. Variance:

   $$\text{Var}(X) = E[X^2] - (E[X])^2 = 38.5 - (5.5)^2 = 38.5 - 30.25 = 8.25$$

Therefore, the variance Var(x) is 8.25.