Question

If the perpendicular sides of a right angled triangle are {$\cos2\alpha + \cos2\beta + 2\cos(\alpha + \beta)$} and {$\sin2\alpha + \sin2\beta + 2\sin(\alpha + \beta)$}, then the length of the hypotenuse is :

• A. 2[1 + cos(α- β)]
• B. 2[1 - cos(α + β)]
• C. 4 $\cos^2 \frac{\alpha - \beta}{2}$
• D. 4$\sin^2 \frac{\alpha + \beta}{2}$

Answer 1

Answer: (A), (C)

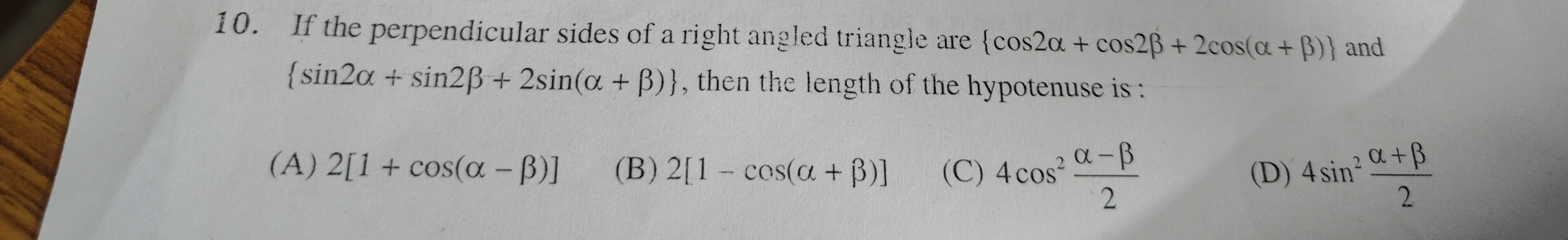
2[1 + cos(α- β)] or 4 $\cos^2 \frac{\alpha - \beta}{2}$

Answer 2

Let the two perpendicular sides of the right-angled triangle be $a$ and $b$.

Given:

$a = \cos2\alpha + \cos2\beta + 2\cos(\alpha + \beta)$

$b = \sin2\alpha + \sin2\beta + 2\sin(\alpha + \beta)$

We will simplify $a$ and $b$ using trigonometric identities.

Recall the sum-to-product formulas:

$\cos A + \cos B = 2\cos\left(\frac{A+B}{2}\right)\cos\left(\frac{A-B}{2}\right)$

$\sin A + \sin B = 2\sin\left(\frac{A+B}{2}\right)\cos\left(\frac{A-B}{2}\right)$

Simplify $a$:

$a = (\cos2\alpha + \cos2\beta) + 2\cos(\alpha + \beta)$

$a = 2\cos\left(\frac{2\alpha+2\beta}{2}\right)\cos\left(\frac{2\alpha-2\beta}{2}\right) + 2\cos(\alpha + \beta)$

$a = 2\cos(\alpha + \beta)\cos(\alpha - \beta) + 2\cos(\alpha + \beta)$

Factor out $2\cos(\alpha + \beta)$:

$a = 2\cos(\alpha + \beta)[\cos(\alpha - \beta) + 1]$

Simplify $b$:

$b = (\sin2\alpha + \sin2\beta) + 2\sin(\alpha + \beta)$

$b = 2\sin\left(\frac{2\alpha+2\beta}{2}\right)\cos\left(\frac{2\alpha-2\beta}{2}\right) + 2\sin(\alpha + \beta)$

$b = 2\sin(\alpha + \beta)\cos(\alpha - \beta) + 2\sin(\alpha + \beta)$

Factor out $2\sin(\alpha + \beta)$:

$b = 2\sin(\alpha + \beta)[\cos(\alpha - \beta) + 1]$

Let $X = \cos(\alpha - \beta) + 1$.

Then, $a = 2\cos(\alpha + \beta)X$ and $b = 2\sin(\alpha + \beta)X$.

The length of the hypotenuse $c$ is given by the Pythagorean theorem: $c = \sqrt{a^2 + b^2}$.

$c^2 = (2\cos(\alpha + \beta)X)^2 + (2\sin(\alpha + \beta)X)^2$

$c^2 = 4\cos^2(\alpha + \beta)X^2 + 4\sin^2(\alpha + \beta)X^2$

Factor out $4X^2$:

$c^2 = 4X^2[\cos^2(\alpha + \beta) + \sin^2(\alpha + \beta)]$

Using the identity $\cos^2\theta + \sin^2\theta = 1$:

$c^2 = 4X^2(1)$

$c^2 = 4X^2$

Taking the square root:

$c = \sqrt{4X^2} = 2|X|$

Substitute back $X = \cos(\alpha - \beta) + 1$:

$c = 2|\cos(\alpha - \beta) + 1|$

Since $-1 \le \cos(\alpha - \beta) \le 1$, it follows that $0 \le \cos(\alpha - \beta) + 1 \le 2$.

Therefore, $\cos(\alpha - \beta) + 1$ is always non-negative, so $|\cos(\alpha - \beta) + 1| = \cos(\alpha - \beta) + 1$.

So, $c = 2[\cos(\alpha - \beta) + 1]$.

We can further simplify this expression using the half-angle identity $1 + \cos\theta = 2\cos^2(\theta/2)$:

$c = 2[2\cos^2\left(\frac{\alpha - \beta}{2}\right)]$

$c = 4\cos^2\left(\frac{\alpha - \beta}{2}\right)$