Solveeit Logo
Login

Question

Question: If $\overline{a}$ = $\hat{i}$+$\hat{j}$-2$\hat{k}$, $\overline{b}$ = 2$\hat{i}$-$\hat{j}$+$\hat{k}$,...

If a‾\overline{a} = i^\hat{i}+j^\hat{j}-2k^\hat{k}, b‾\overline{b} = 2i^\hat{i}-j^\hat{j}+k^\hat{k}, c‾\overline{c} = 3i^\hat{i}-k^\hat{k} and

c‾\overline{c} = ma‾\overline{a}+nb‾\overline{b}, then m + n =

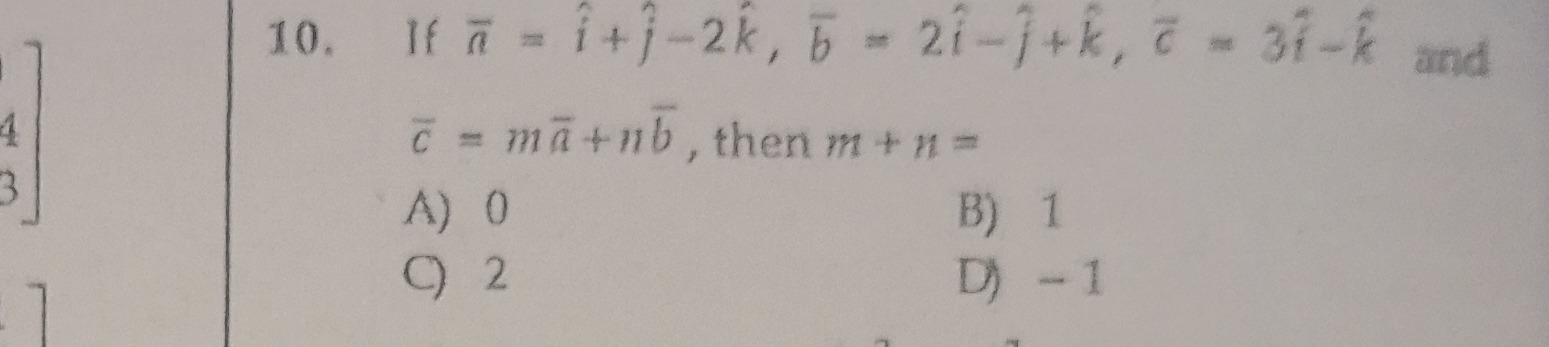
A

0

B

1

C

2

D

-1

Answer

2

Explanation

Solution

Given

a‾=⟨1,1,−2⟩,b‾=⟨2,−1,1⟩,c‾=⟨3,0,−1⟩\overline{a} = \langle 1, 1, -2 \rangle,\quad \overline{b} = \langle 2, -1, 1 \rangle,\quad \overline{c} = \langle 3, 0, -1 \rangle

and

c‾=m a‾+n b‾.\overline{c} = m\,\overline{a} + n\,\overline{b}.

Writing component-wise:

  • xx-component: m+2n=3m + 2n = 3
  • yy-component: m−n=0m - n = 0
  • zz-component: −2m+n=−1-2m + n = -1

From m−n=0m - n = 0, we have m=nm = n.

Substitute n=mn = m in the xx-component:

m+2m=3⇒3m=3⇒m=1.m + 2m = 3 \Rightarrow 3m = 3 \Rightarrow m = 1.

Thus, n=1n = 1.

Therefore, m+n=1+1=2.m + n = 1 + 1 = 2.