Question

10. If log (x + y) = log (xy) + 3, then dy/dx =

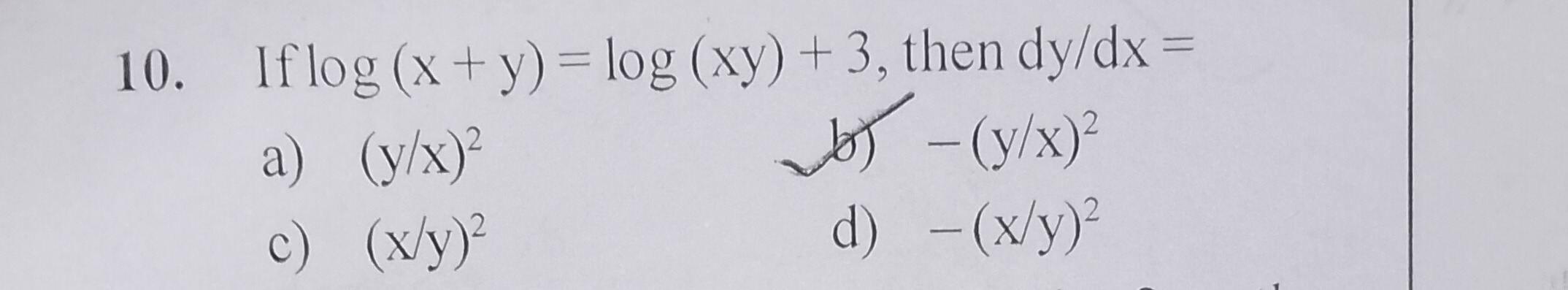
• A. $(y/x)^2$
• B. $-(y/x)^2$
• C. $(x/y)^2$
• D. $-(x/y)^2$

Answer 1

Answer: (B)

-(y/x)^2

Answer 2

Given

$$\log(x+y) = \log (xy) + 3,$$

differentiate both sides with respect to $x$. Using the chain rule:

$$\frac{1}{x+y}(1+\frac{dy}{dx}) = \frac{1}{xy}\left(y + x\frac{dy}{dx}\right).$$

Multiplying both sides by $xy(x+y)$ gives:

$$xy(1+\frac{dy}{dx}) = (x+y)(y + x\frac{dy}{dx}).$$

Expanding and simplifying:

$$xy + xy\frac{dy}{dx} = xy + y^2 + x^2\frac{dy}{dx} + xy\frac{dy}{dx}.$$

Cancel $xy$ and $xy\frac{dy}{dx}$ from both sides:

$$0 = y^2 + x^2\frac{dy}{dx}.$$

Thus,

$$\frac{dy}{dx} = -\frac{y^2}{x^2} = -\left(\frac{y}{x}\right)^2.$$