Question
Question: If $\frac{x-1}{x^2+2x+a}$ takes all real values for possible values of x, then find $a$....
If x2+2x+ax−1 takes all real values for possible values of x, then find a.
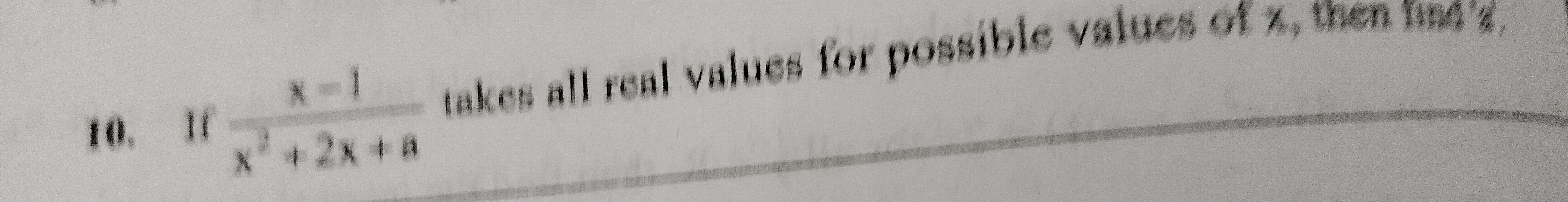
-3
Solution
Let y=x2+2x+ax−1. For y to take all real values, the equation y(x2+2x+a)=x−1 must have real solutions for x for every real value of y, provided the denominator is non-zero.
Rearranging, we get yx2+(2y−1)x+(ay+1)=0.
For y=0, this is a quadratic in x. It has real roots if the discriminant Δ=(2y−1)2−4y(ay+1)≥0.
Δ=(4−4a)y2−8y+1.
For Δ≥0 for all y=0, the quadratic in y must satisfy 4−4a≥0 and (−8)2−4(4−4a)(1)≤0.
a≤1 and 64−16+16a≤0⟹48+16a≤0⟹a≤−3.
Thus, for y=0, real roots exist if a≤−3.
For y=0, the equation is −x+1=0, so x=1. For y=0 to be in the range, the denominator at x=1 must be non-zero: 12+2(1)+a=3+a=0, so a=−3.
Combining the conditions for all real y to be possible, we need a≤−3 and a=−3, which means a<−3.
If a<−3, the range is R.
If a=−3, the range is R∖{0,1/4}.
The question asks for "find a", implying a specific value. The value a=−3 is the boundary between the region where the range is R (a<−3) and where it is not. Assuming the question expects this critical value, the answer is -3.
