Question

f(x) = 2024 + \sqrt{2x - 1 + 2\sqrt{x^2 - x}} ;-;\sqrt{x - 1}

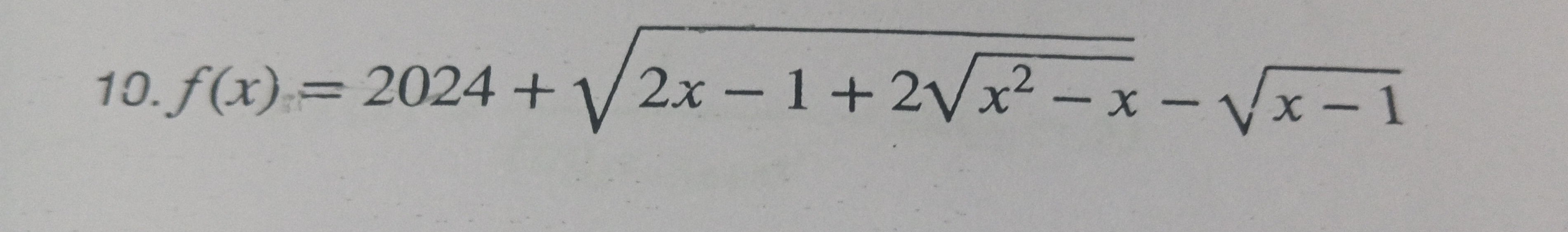
Answer 1

2024 + \sqrt{x}, \quad x \ge 1

Answer 2

Step 1. Recognise the perfect square under the first square root

$$2x - 1 + 2\sqrt{x^2 - x} = (\sqrt{x} + \sqrt{x - 1})^2.$$

Step 2. Therefore,

$$\sqrt{2x - 1 + 2\sqrt{x^2 - x}} = \sqrt{(\sqrt{x} + \sqrt{x - 1})^2} = \sqrt{x} + \sqrt{x - 1},$$

valid for $x\ge1$.

Step 3. Substitute back into $f(x)$:

$$f(x) = 2024 + \bigl(\sqrt{x} + \sqrt{x - 1}\bigr) - \sqrt{x - 1} = 2024 + \sqrt{x}.$$

Conclusion. The simplified form is

$$f(x)=2024+\sqrt{x},\quad x\ge1.$$