Question
Question: Find the sum to $n$ terms of the series, $$1+\left(1+\frac{1}{2}+\frac{1}{2^2}\right)+\left(1+\frac{...
Find the sum to n terms of the series, 1+(1+21+221)+(1+21+221+231+241)+…
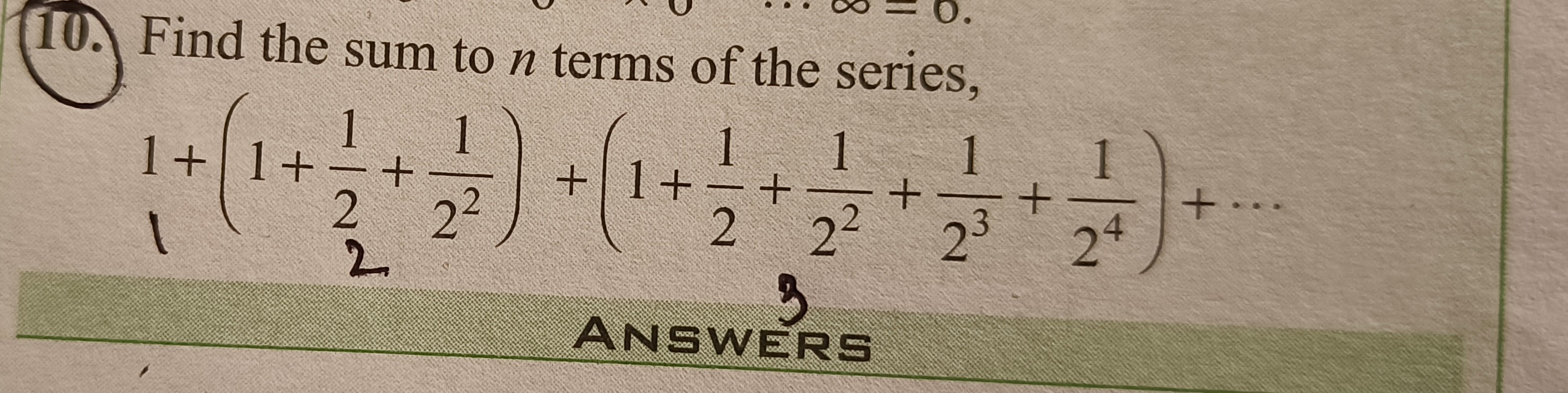
Answer
2n - \frac{4}{3} + \frac{1}{3 \cdot 4^{n-1}}
Explanation
Solution
The k-th term of the series, Tk, is identified as a geometric progression with first term 1, common ratio 1/2, and 2k−1 terms. Its sum is found using the GP sum formula to be Tk=2−22k−21. The sum of the series to n terms, Sn=∑k=1nTk, is then calculated. This sum simplifies to 2n−∑k=1n4k−11. The second part is another geometric progression with first term 1, common ratio 1/4, and n terms. Its sum is 34−3⋅4n−11. Substituting this back yields the final expression for Sn.
