Question
Question: Find the moment of inertia of the two uniform joint rods about an axis passing through P perpendicul...
Find the moment of inertia of the two uniform joint rods about an axis passing through P perpendicular to plane of paper (mass of each rod = m and length of each rod = l)
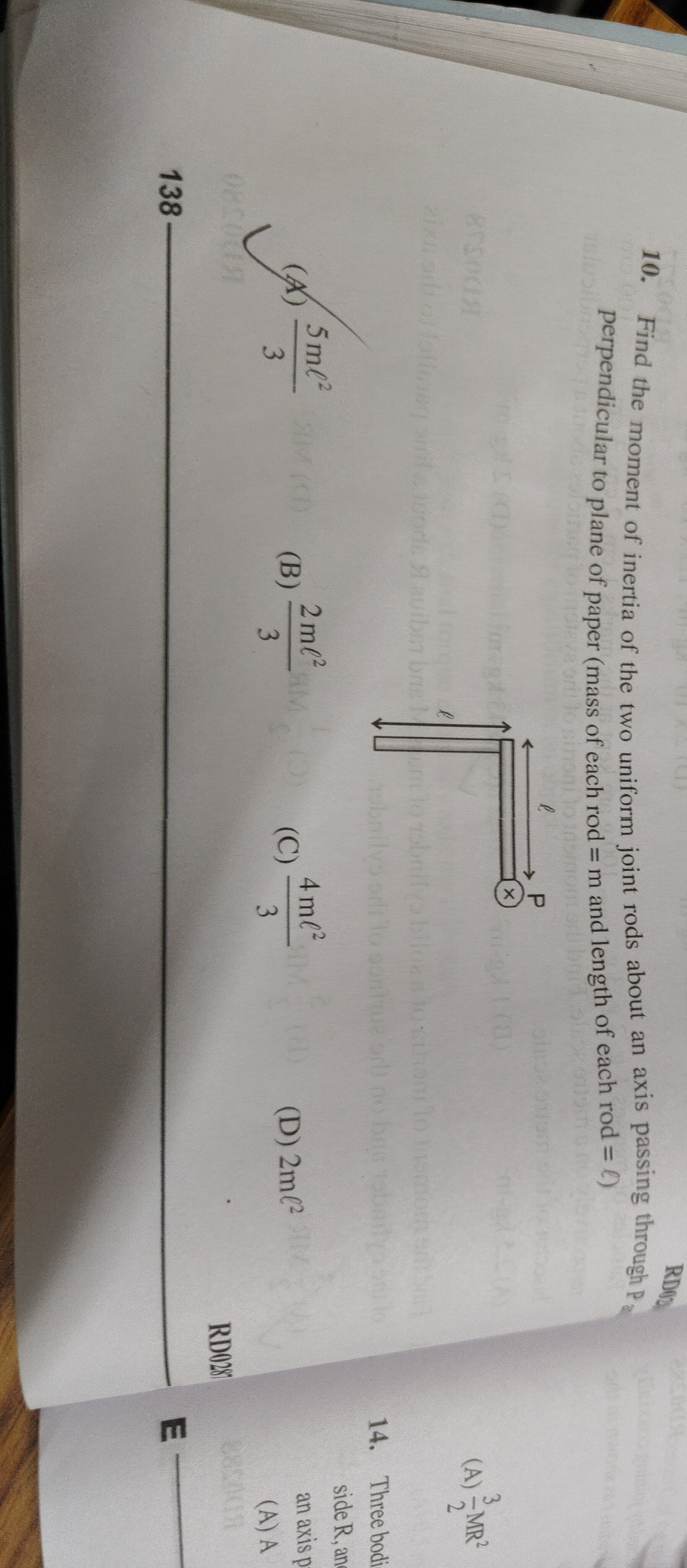
35ml2
32ml2
34ml2
2ml2
32ml2
Solution
To find the moment of inertia of the two uniform joint rods about an axis passing through P perpendicular to the plane of the paper, we can treat each rod separately and then sum their individual moments of inertia.
Let's label the rods:
-
Rod 1 (Vertical Rod): This rod has mass m and length l. The axis of rotation passes through point P, which is at one end of this rod. Since the axis is perpendicular to the plane of the paper, it is also perpendicular to the length of this rod. The moment of inertia of a uniform rod of mass M and length L about an axis passing through its end and perpendicular to its length is given by: Iend=3ML2 For Rod 1, M=m and L=l. So, the moment of inertia of Rod 1 about the axis through P is: I1=3ml2
-
Rod 2 (Horizontal Rod): This rod also has mass m and length l. The axis of rotation passes through point P, which is at one end of this rod. Since the axis is perpendicular to the plane of the paper, it is also perpendicular to the length of this rod. Similarly, for Rod 2, M=m and L=l. So, the moment of inertia of Rod 2 about the axis through P is: I2=3ml2
The total moment of inertia of the system is the sum of the moments of inertia of the individual rods, as moment of inertia is an additive scalar quantity: Itotal=I1+I2 Itotal=3ml2+3ml2 Itotal=32ml2
