Question

Find the equation of the tangent to the circle $x^2 + y^2 = 25$, which are inclined at $30^\circ$ to the axis of x.

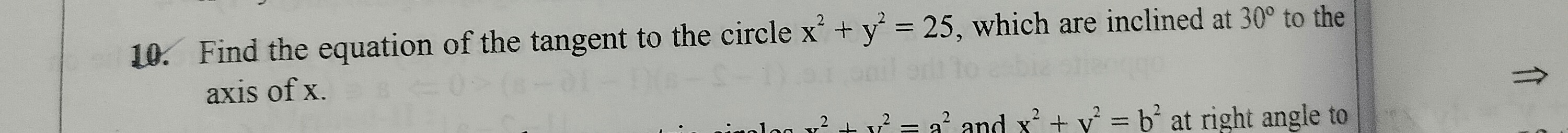
Answer 1

The equations of the tangents are: $x - \sqrt{3}y + 10 = 0$ $x - \sqrt{3}y - 10 = 0$

Answer 2

The equation of the circle is $x^2 + y^2 = 25$, which is centered at the origin $(0,0)$ with a radius $r = 5$. The tangents are inclined at $30^\circ$ to the x-axis, so the slope $m = \tan(30^\circ) = \frac{1}{\sqrt{3}}$. The general equation of a tangent to the circle $x^2 + y^2 = r^2$ with slope $m$ is $y = mx \pm r\sqrt{1+m^2}$. Substituting $m = \frac{1}{\sqrt{3}}$ and $r=5$: $y = \frac{1}{\sqrt{3}}x \pm 5\sqrt{1+\left(\frac{1}{\sqrt{3}}\right)^2}$ $y = \frac{x}{\sqrt{3}} \pm 5\sqrt{1+\frac{1}{3}}$ $y = \frac{x}{\sqrt{3}} \pm 5\sqrt{\frac{4}{3}}$ $y = \frac{x}{\sqrt{3}} \pm 5\left(\frac{2}{\sqrt{3}}\right)$ $y = \frac{x}{\sqrt{3}} \pm \frac{10}{\sqrt{3}}$ Multiplying by $\sqrt{3}$: $\sqrt{3}y = x \pm 10$ Rearranging gives the equations of the tangents: $x - \sqrt{3}y \pm 10 = 0$. Thus, the two equations are $x - \sqrt{3}y + 10 = 0$ and $x - \sqrt{3}y - 10 = 0$.