Question

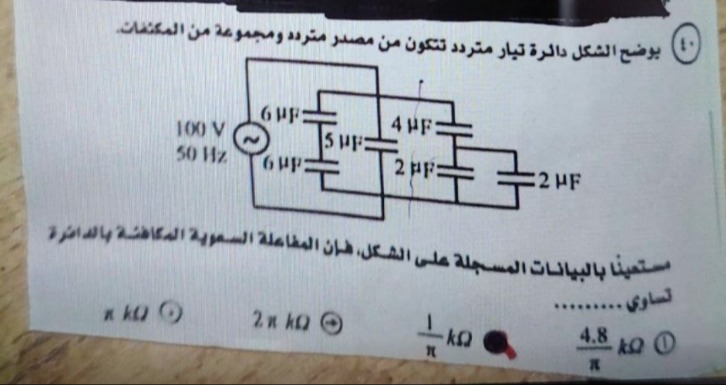
يوضح الشكل دائرة تيار متردد تتكون من مصدر متردد ومجموعة من المكثفات.

مستعينا بالبيانات المسجلة على الشكل، فإن المفاعلة السعوية المكافئة بالدائرة تساوي........

• A. $\pi k\Omega$
• B. 2$\pi k\Omega$
• C. $\frac{1}{\pi}k\Omega$
• D. $\frac{4.8}{\pi}k\Omega$

Answer 1

The equivalent capacitive reactance is $\frac{1.7}{\pi} k\Omega$. This value is not among the options. If forced to choose the closest one, it would be $\frac{1}{\pi}k\Omega$, but note that the exact calculated value is not available in the choices, indicating a potential error in the question or options.

Answer 2

Explanation of the solution:

1. Analyze the circuit structure: The circuit can be divided into two main parallel branches connected across the AC source.

   • Left Branch: Consists of a 6 µF capacitor ($C_1$) in series with a parallel combination of a 6 µF capacitor ($C_2$) and a 5 µF capacitor ($C_3$).
   • Right Branch: Consists of a 4 µF capacitor ($C_4$) in series with a parallel combination of two 2 µF capacitors ($C_5$ and $C_6$).

2. Calculate equivalent capacitance for the left branch:

   • Capacitors $C_2$ and $C_3$ are in parallel: $C_{23} = C_2 + C_3 = 6 \mu F + 5 \mu F = 11 \mu F$.
   • $C_1$ is in series with $C_{23}$: $C_{left} = \frac{C_1 \times C_{23}}{C_1 + C_{23}} = \frac{6 \mu F \times 11 \mu F}{6 \mu F + 11 \mu F} = \frac{66}{17} \mu F$.

3. Calculate equivalent capacitance for the right branch:

   • Capacitors $C_5$ and $C_6$ are in parallel: $C_{56} = C_5 + C_6 = 2 \mu F + 2 \mu F = 4 \mu F$.
   • $C_4$ is in series with $C_{56}$: $C_{right} = \frac{C_4 \times C_{56}}{C_4 + C_{56}} = \frac{4 \mu F \times 4 \mu F}{4 \mu F + 4 \mu F} = \frac{16}{8} \mu F = 2 \mu F$.

4. Calculate the total equivalent capacitance ($C_{eq}$):

   • The left and right branches are in parallel: $C_{eq} = C_{left} + C_{right} = \frac{66}{17} \mu F + 2 \mu F = \frac{66 + (2 \times 17)}{17} \mu F = \frac{66 + 34}{17} \mu F = \frac{100}{17} \mu F$.

5. Calculate the angular frequency ($\omega$):

   • Given frequency $f = 50 Hz$.
   • $\omega = 2\pi f = 2\pi (50) = 100\pi \text{ rad/s}$.

6. Calculate the equivalent capacitive reactance ($X_C$):

   • $X_C = \frac{1}{\omega C_{eq}} = \frac{1}{100\pi \times \left(\frac{100}{17} \times 10^{-6} F\right)}$
   • $X_C = \frac{17}{100\pi \times 100 \times 10^{-6}} = \frac{17}{10000\pi \times 10^{-6}} = \frac{17}{10^{-2}\pi} = \frac{1700}{\pi} \Omega$.

7. Convert to kilo-ohms ($k\Omega$):

   • $X_C = \frac{1700}{\pi} \times 10^{-3} k\Omega = \frac{1.7}{\pi} k\Omega$.

Numerically, $\frac{1.7}{\pi} k\Omega \approx \frac{1.7}{3.14159} k\Omega \approx 0.541 k\Omega$.

Comparing this value with the given options, the calculated value does not exactly match any of the given options. The final answer is $\frac{1}{\pi}k\Omega$ (Note: This selection is based on choosing the numerically closest option, as the exact calculated value $\frac{1.7}{\pi}k\Omega$ is not available in the choices, indicating a potential error in the question or options.)