Question

$e^x \tan y \, dx + (1 - e^x) \sec^2 y \, dy = 0$

Answer 1

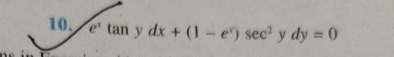
$\tan y = C(1 - e^x)$

Answer 2

The given differential equation is: $e^x \tan y \, dx + (1 - e^x) \sec^2 y \, dy = 0$

This is a first-order differential equation. We can solve it using the variable separable method.

Step 1: Separate the variables. Rearrange the terms to group $x$ terms with $dx$ and $y$ terms with $dy$: $e^x \tan y \, dx = - (1 - e^x) \sec^2 y \, dy$ Divide both sides by $\tan y$ and $(1 - e^x)$ to separate the variables: $\frac{e^x}{1 - e^x} \, dx = - \frac{\sec^2 y}{\tan y} \, dy$

Step 2: Integrate both sides. $\int \frac{e^x}{1 - e^x} \, dx = \int - \frac{\sec^2 y}{\tan y} \, dy$

For the left-hand side integral, let $u = 1 - e^x$. Then, differentiate $u$ with respect to $x$: $du = -e^x \, dx$ So, $e^x \, dx = -du$. The integral becomes: $\int \frac{-du}{u} = - \ln |u| + C_1 = - \ln |1 - e^x| + C_1$

For the right-hand side integral, let $v = \tan y$. Then, differentiate $v$ with respect to $y$: $dv = \sec^2 y \, dy$ The integral becomes: $\int - \frac{dv}{v} = - \ln |v| + C_2 = - \ln |\tan y| + C_2$

Step 3: Combine the results and simplify. Equating the results of the integrals: $- \ln |1 - e^x| + C_1 = - \ln |\tan y| + C_2$ Rearrange the terms: $\ln |\tan y| - \ln |1 - e^x| = C_2 - C_1$ Let $C = C_2 - C_1$ be an arbitrary constant. $\ln \left| \frac{\tan y}{1 - e^x} \right| = C$ To remove the logarithm, take the exponential of both sides: $\left| \frac{\tan y}{1 - e^x} \right| = e^C$ Let $A = e^C$. Since $C$ is an arbitrary constant, $A$ is an arbitrary positive constant. $\frac{\tan y}{1 - e^x} = \pm A$ Let $K = \pm A$. $K$ is an arbitrary non-zero constant. $\frac{\tan y}{1 - e^x} = K$ $\tan y = K (1 - e^x)$ This is the general solution. The constant $K$ can also be zero, which corresponds to the solution $\tan y = 0$, or $y = n\pi$ for integer $n$. This solution is also covered by the original differential equation if $1-e^x \neq 0$. Thus, $K$ is an arbitrary constant.

The final solution is: $\tan y = C (1 - e^x)$ (where $C$ is an arbitrary constant)