Question

Coefficient of $x^{12}$ in the expansion of $(1 + x^2)^{50} (x + \frac{1}{x})^{-10}$

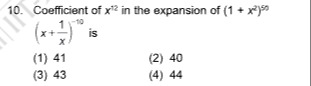
• A. 41
• B. 40
• C. 43
• D. 44

Answer 1

Answer: (B)

40

Answer 2

The given expression is $(1 + x^2)^{50} (x + \frac{1}{x})^{-10}$. Simplify the expression: $(1 + x^2)^{50} (\frac{x^2+1}{x})^{-10} = (1 + x^2)^{50} (\frac{x}{x^2+1})^{10} = (1 + x^2)^{50} \frac{x^{10}}{(x^2+1)^{10}}$ $= x^{10} (1 + x^2)^{50-10} = x^{10} (1 + x^2)^{40}$. We need the coefficient of $x^{12}$ in $x^{10} (1 + x^2)^{40}$. This means we need the coefficient of $x^{12-10} = x^2$ in the expansion of $(1 + x^2)^{40}$. The general term in the expansion of $(1 + y)^n$ is $\binom{n}{k} y^k$. For $(1 + x^2)^{40}$, the general term is $\binom{40}{k} (x^2)^k = \binom{40}{k} x^{2k}$. To find the term with $x^2$, we set $2k = 2$, which gives $k = 1$. The coefficient of $x^2$ is $\binom{40}{1} = 40$. Thus, the coefficient of $x^{12}$ is 40.