Question
Question: A string is pulled with a force F = 130 N as shown. The force vector comes out to be $\overrightarr...
A string is pulled with a force F = 130 N as shown. The force vector comes out to be
F = 10 (αi^ + βj^ + γk^) N. Write β + α + γ in OMR sheet.
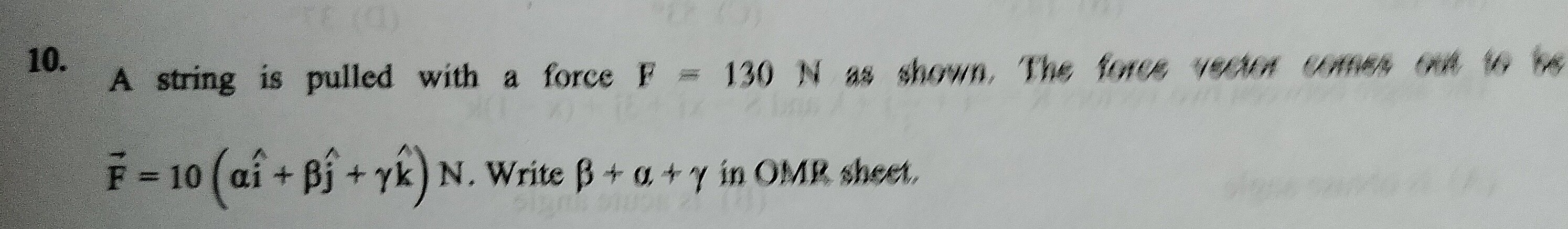
13
Solution
The force vector F is directed from the origin O(0, 0, 0) to the point P(12, 4, -3).
The position vector of point P relative to the origin is r=OP=(12−0)i^+(4−0)j^+(−3−0)k^=12i^+4j^−3k^.
The magnitude of this position vector is ∣r∣=122+42+(−3)2=144+16+9=169=13.
The unit vector in the direction of F is r^=∣r∣r=1312i^+4j^−3k^.
The magnitude of the force is given as F=130 N.
The force vector F can be written as the product of its magnitude and the unit vector in its direction: F=Fr^=130×1312i^+4j^−3k^. F=10×(12i^+4j^−3k^)=120i^+40j^−30k^.
The problem states that the force vector is given by F = 10 (αi^ + βj^ + γk^) N.
Comparing this form with the calculated force vector: 10(αi^+βj^+γk^)=10(12i^+4j^−3k^).
Dividing by 10 on both sides: αi^ + βj^ + γk^ = 12i^+4j^−3k^.
Comparing the coefficients of i^, j^, and k^: α=12 β=4 γ=−3
We need to find the value of β+α+γ. β+α+γ=4+12+(−3)=16−3=13.
