Question

A strictly increasing sequence of positive integers a, b, c satisfies the property that $\frac{a+b}{2}$, $\frac{a+c}{2}$, $\frac{b+c}{2}$ form a geometric sequence. What is the smallest possible value of a + b + c?

Answer 1

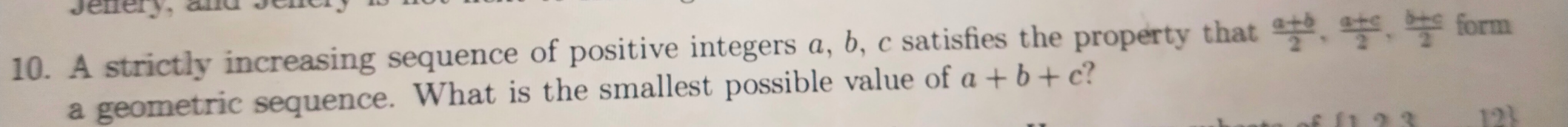
19

Answer 2

We are given that

$$\frac{a+b}{2},\quad \frac{a+c}{2},\quad \frac{b+c}{2}$$

form a geometric progression. Hence the middle term squared equals the product of the extreme terms:

$$\Bigl(\frac{a+c}{2}\Bigr)^2=\frac{a+b}{2}\cdot\frac{b+c}{2}.$$

Multiplying both sides by 4 gives

$$(a+c)^2 = (a+b)(b+c).$$

One clever method is to “reverse‐engineer” the three numbers. Introduce a parameter $x$ and a ratio $r$ (with $r>1$ since $a<b<c$) by writing

$$\frac{a+b}{2}=x,\quad \frac{a+c}{2}=xr,\quad \frac{b+c}{2}=xr^2.$$

Then

$$a+b=2x,\quad a+c=2xr,\quad b+c=2xr^2.$$

We can solve for $a,\,b,\,c$ by adding and subtracting. Adding the first two gives

$$2a+b+c=2x+2xr,$$

and since $b+c=2xr^2$ we get

$$2a=2x+2xr-2xr^2,\quad \Rightarrow\quad a=x(1+r-r^2).$$

Similarly, subtracting $a$ from $a+b$ yields

$$b=2x-a =2x-x(1+r-r^2)=x(1 - r + r^2),$$

and from $a+c$ we have

$$c=2xr-a=x(2r-1-r+r^2)=x(r+r^2-1).$$

For these to be positive integers, the expressions

$$x(1+r-r^2),\quad x(1-r+r^2),\quad x(r+r^2-1)$$

must be positive integers. It is natural to try a rational $r=\frac{p}{q}$ (in lowest terms) and choose $x$ to clear denominators.

A good choice is $r=\frac{3}{2}$ (since $r>1$). Then

$$a=x\Bigl(1+\frac{3}{2}-\frac{9}{4}\Bigr)=x\Bigl(\frac{4+6-9}{4}\Bigr)=\frac{x}{4},$$ $$b=x\Bigl(1-\frac{3}{2}+\frac{9}{4}\Bigr)=x\Bigl(\frac{4-6+9}{4}\Bigr)=\frac{7x}{4},$$ $$c=x\Bigl(\frac{3}{2}+\frac{9}{4}-1\Bigr)=x\Bigl(\frac{6+9-4}{4}\Bigr)=\frac{11x}{4}.$$

For $a$, $b$, and $c$ to be integers we choose the smallest $x$ such that $x/4$ is an integer. Taking $x=4$ yields

$$a=1,\quad b=7,\quad c=11.$$

Then

$$a+b+c=1+7+11=19.$$

Finally, we check the given condition:

$$\frac{a+b}{2}=\frac{1+7}{2}=4,\quad \frac{a+c}{2}=\frac{1+11}{2}=6,\quad \frac{b+c}{2}=\frac{7+11}{2}=9,$$

which form a G.P. with common ratio $\frac{6}{4}=\frac{9}{6}=\frac{3}{2}$.

Thus, the smallest possible value of $a+b+c$ is 19.

---

Summary (Minimal Explanation):

1. For numbers $\frac{a+b}{2}$, $\frac{a+c}{2}$, $\frac{b+c}{2}$ in G.P., we have $(a+c)^2=(a+b)(b+c)$.

2. By writing $\frac{a+b}{2}=x$, $\frac{a+c}{2}=xr$, $\frac{b+c}{2}=xr^2$ and solving, we get

$$a=x(1+r-r^2),\quad b=x(1-r+r^2),\quad c=x(r+r^2-1).$$

3. Choosing $r=\frac{3}{2}$ and $x=4$ yields $a=1$, $b=7$, $c=11$ and hence $a+b+c=19$.