Question

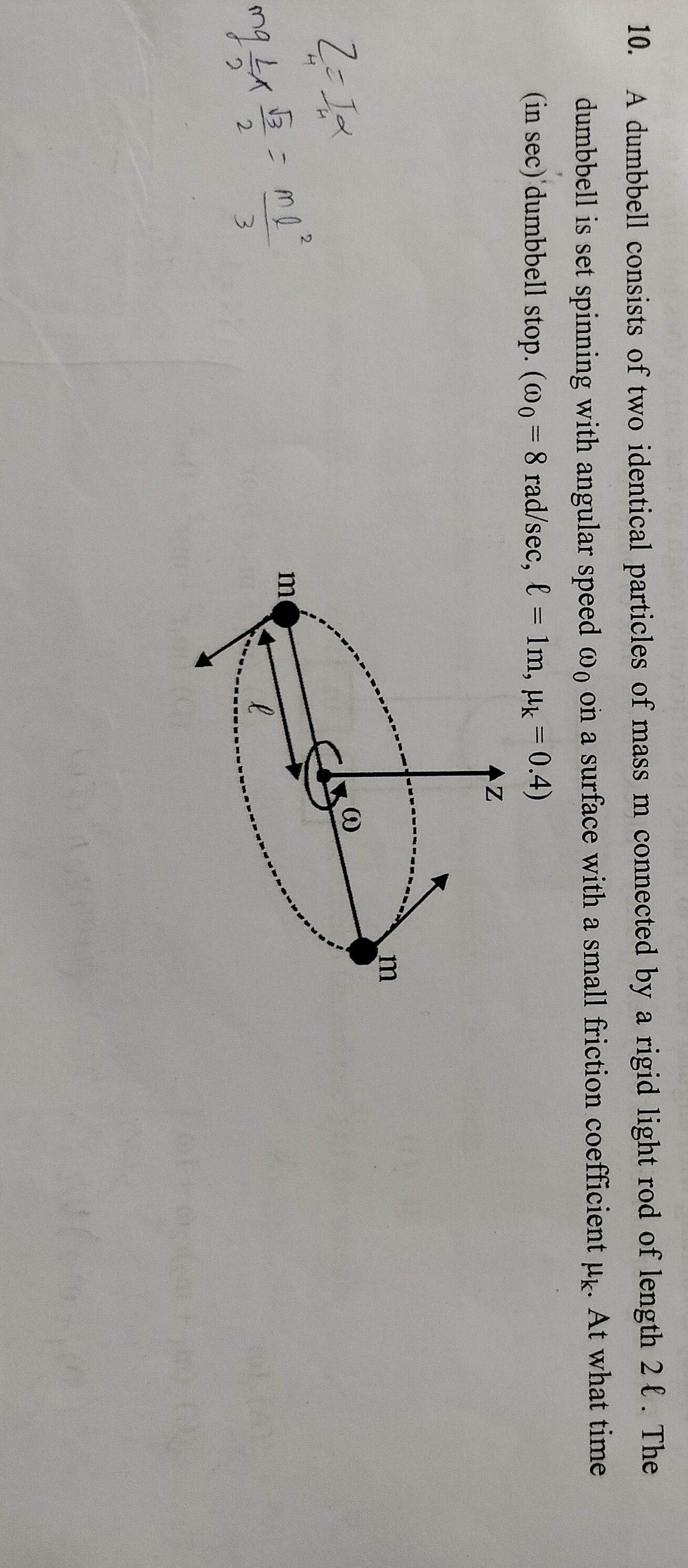
A dumbbell consists of two identical particles of mass m connected by a rigid light rod of length 2 l. The dumbbell is set spinning with angular speed $\omega_0$ on a surface with a small friction coefficient $\mu_k$. At what time (in sec) dumbbell stop. ($\omega_0$ = 8 rad/sec, l = 1m, $\mu_k$ = 0.4)

Answer 1

2.04

Answer 2

The dumbbell consists of two identical particles of mass $m$ at a distance $l$ from the center, connected by a light rod of length $2l$. The axis of rotation passes through the center of the rod.

1. Moment of Inertia (I): The moment of inertia of the dumbbell about the axis of rotation is the sum of the moments of inertia of the two particles. For a point mass $m$ at a distance $r$ from the axis, $I = mr^2$. Therefore, $I = m(l)^2 + m(l)^2 = 2ml^2$.

2. Frictional Torque ($\tau$): The kinetic friction force on each particle is $f_k = \mu_k N$, where $N$ is the normal force. Since the particles are on a surface, $N = mg$. So, $f_k = \mu_k mg$. This friction force acts tangentially, opposing the motion, at a distance $l$ from the axis of rotation. The torque due to friction on one particle is $\tau_1 = f_k \times l = (\mu_k mg) \times l$. Since there are two such particles, the total frictional torque is $\tau = 2 \times (\mu_k mgl) = 2\mu_k mgl$. This torque causes angular deceleration.

3. Angular Deceleration ($\alpha$): Using Newton's second law for rotation, $\tau = I\alpha$. The torque opposes the angular velocity, so we consider its magnitude. $\alpha = \frac{\tau}{I} = \frac{2\mu_k mgl}{2ml^2} = \frac{\mu_k g}{l}$.

4. Time to Stop (t): We use the rotational kinematic equation $\omega_f = \omega_0 + \alpha t$, where $\omega_f$ is the final angular velocity, $\omega_0$ is the initial angular velocity, and $\alpha$ is the angular acceleration. Since the dumbbell stops, $\omega_f = 0$. The acceleration is negative as it opposes the motion. $0 = \omega_0 - \alpha t$ $t = \frac{\omega_0}{\alpha} = \frac{\omega_0}{\frac{\mu_k g}{l}} = \frac{\omega_0 l}{\mu_k g}$.

5. Given Values: $\omega_0 = 8$ rad/sec $l = 1$ m $\mu_k = 0.4$ We use the standard value for acceleration due to gravity, $g = 9.8$ m/s².

6. Calculation: $t = \frac{8 \text{ rad/sec} \times 1 \text{ m}}{0.4 \times 9.8 \text{ m/s}^2} = \frac{8}{3.92} \text{ sec} \approx 2.04 \text{ sec}$.