Question
Question: Solve for x: $\frac{1}{x-1} - \frac{4}{x-2} + \frac{4}{x-3} - \frac{1}{x-4} = \frac{1}{30}$ ...
Solve for x:
x−11−x−24+x−34−x−41=301
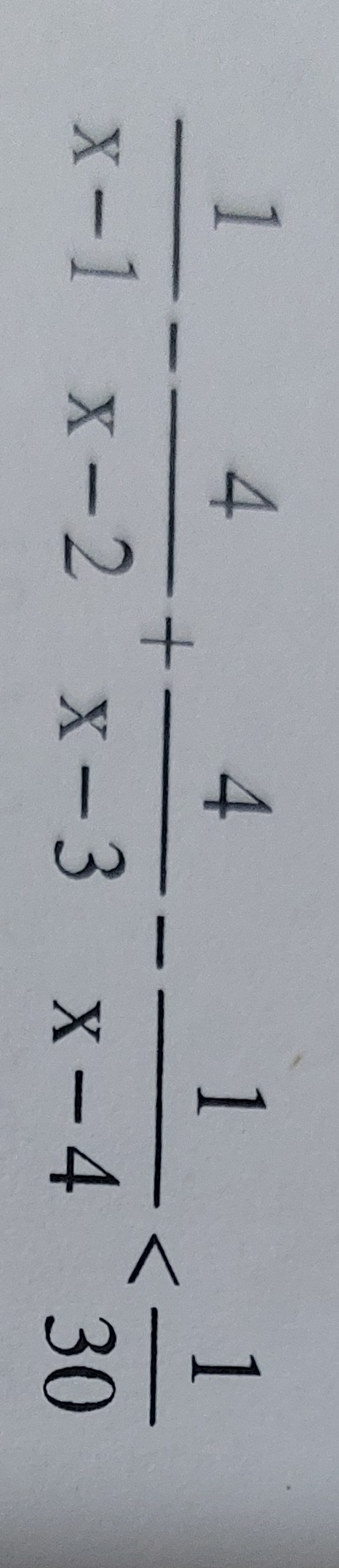
-2, -1, 6, 7
Solution
The given equation is x−11−x−24+x−34−x−41=301 We group the terms as follows: (x−11−x−41)−(x−24−x−34)=301 Combine the terms in each group: (x−1)(x−4)(x−4)−(x−1)−4(x−21−x−31)=301 (x−1)(x−4)x−4−x+1−4((x−2)(x−3)(x−3)−(x−2))=301 x2−5x+4−3−4(x2−5x+6x−3−x+2)=301 x2−5x+4−3−4(x2−5x+6−1)=301 x2−5x+4−3+x2−5x+64=301 Let y=x2−5x. The equation becomes: y+4−3+y+64=301 Combine the terms on the left side: (y+4)(y+6)−3(y+6)+4(y+4)=301 y2+10y+24−3y−18+4y+16=301 y2+10y+24y−2=301 Cross-multiply: 30(y−2)=y2+10y+24 30y−60=y2+10y+24 Rearrange into a quadratic equation in y: y2+10y−30y+24+60=0 y2−20y+84=0 Factor the quadratic equation: (y−6)(y−14)=0 So, y=6 or y=14. Substitute back y=x2−5x.
Case 1: x2−5x=6 x2−5x−6=0 (x−6)(x+1)=0 So, x=6 or x=−1.
Case 2: x2−5x=14 x2−5x−14=0 (x−7)(x+2)=0 So, x=7 or x=−2.
The possible values for x are -2, -1, 6, and 7. We check that none of these values make the original denominators zero. The denominators are x−1,x−2,x−3,x−4. None of the values -2, -1, 6, 7 are equal to 1, 2, 3, or 4. Thus, all four solutions are valid.
