Question
Question: The value of current in the 6$\Omega$ resistance is :...
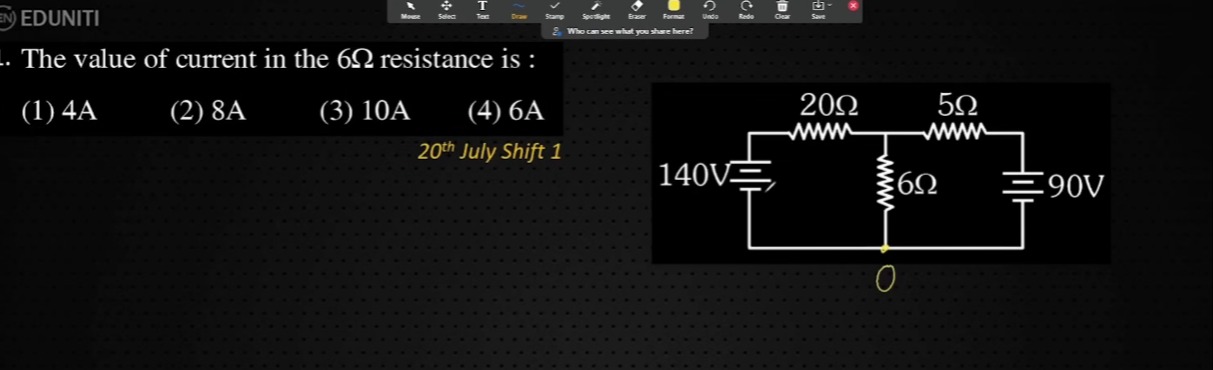
The value of current in the 6Ω resistance is :
A
4A
B
8A
C
10A
D
6A
Answer
10A
Explanation
Solution
The problem can be solved using nodal analysis.
- Assign Node Potentials: Let the common bottom wire be the reference node with potential V=0. Let the junction point between the 20Ω, 5Ω, and 6Ω resistors be node A, with potential VA.
- Apply Kirchhoff's Current Law (KCL) at Node A:
- Current flowing from the 140V source through the 20Ω resistor to node A: I1=20140−VA.
- Current flowing from node A through the 6Ω resistor to the reference node (0V): I2=6VA−0=6VA.
- Current flowing from node A through the 5Ω resistor to the positive terminal of the 90V source (which is at 90V relative to the reference): I3=5VA−90.
- Formulate the KCL Equation: Assuming currents I1 enters node A and currents I2 and I3 leave node A, the KCL equation is I1=I2+I3. 20140−VA=6VA+5VA−90
- Solve for VA: Multiply the equation by the least common multiple of the denominators (20, 6, 5), which is 60: 60(20140−VA)=60(6VA)+60(5VA−90) 3(140−VA)=10VA+12(VA−90) 420−3VA=10VA+12VA−1080 420−3VA=22VA−1080 420+1080=22VA+3VA 1500=25VA VA=251500=60 V
- Calculate the Current through the 6Ω Resistance: The current through the 6Ω resistance is I2: I6Ω=6VA=6Ω60 V=10 A
