Solveeit Logo
Login

Question

Question: The roots of the equation $(b - c) x^2 + (c - a) x + (a - b) = 0$ are...

The roots of the equation (b−c)x2+(c−a)x+(a−b)=0(b - c) x^2 + (c - a) x + (a - b) = 0 are

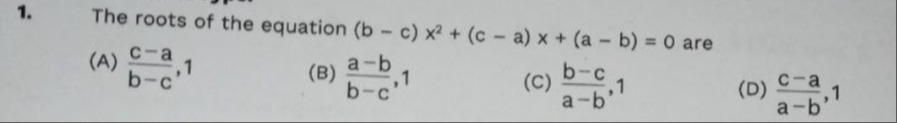
A

c−ab−c,1\frac{c-a}{b-c},1

B

a−bb−c,1\frac{a-b}{b-c},1

C

b−ca−b,1\frac{b-c}{a-b},1

D

c−aa−b,1\frac{c-a}{a-b},1

Answer

Option (B)

Explanation

Solution

Given the quadratic equation

(b−c)x2+(c−a)x+(a−b)=0.(b-c)x^2 + (c-a)x + (a-b)=0.

  1. Substitute x=1x=1:

    (b−c)+(c−a)+(a−b)=0.(b-c) + (c-a) + (a-b) = 0.

    Thus, x=1x=1 is a root.

  2. Factorizing, assume

    (b−c)x2+(c−a)x+(a−b)=(x−1)(Ax+B).(b-c)x^2 + (c-a)x + (a-b) = (x-1)(Ax+B).

    Expanding the right side:

    Ax2+Bx−Ax−B=Ax2+(B−A)x−B.Ax^2 + Bx - Ax - B = Ax^2 + (B-A)x - B.

    Matching coefficients:

    A=b−c,B−A=c−a  ⟹  B=c−a+(b−c)=b−a,−B=a−b.A = b-c,\quad B-A = c-a \implies B = c-a+(b-c)=b-a, \quad -B = a-b.

  3. For the second root, set the factor Ax+B=0Ax+B=0:

    (b−c)x+(b−a)=0⟹x=−(b−a)b−c=a−bb−c.(b-c)x + (b-a)=0 \quad \Longrightarrow \quad x = \frac{-(b-a)}{b-c} = \frac{a-b}{b-c}.

Thus, the roots are a−bb−c\frac{a-b}{b-c} and 11.