Question
Question: The moment of inertia of a uniform rod of mass $m$ and length $l$ is $\alpha$ when rotated about an ...
The moment of inertia of a uniform rod of mass m and length l is α when rotated about an axis passing through centre and perpendicular to the length. If the rod is broken into equal halves and arranged as shown, then the moment of inertia about the given axis is
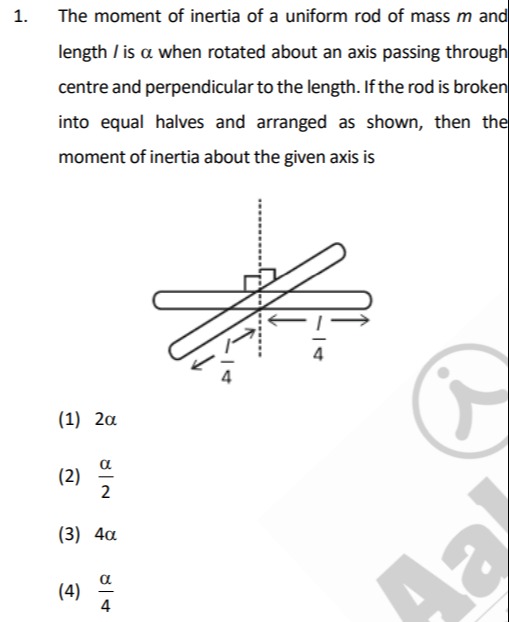
2α
2α
4α
4α
α
Solution
We start by noting that for a uniform rod of mass m and length l, the moment of inertia about an axis perpendicular to its length through its centre is
Irod=121ml2=α.Now the rod is broken into two equal halves. Each half has mass = m/2 and length = l/2.
For a thin rod of length L and mass M, the moment of inertia about an axis through its centre (and perpendicular to it) is Icm=121ML2.
Thus for one half‐rod we have
Icm(half)=121(2m)(2l)2=121⋅2m⋅4l2=96ml2.According to the diagram each half–rod is located so that its centre of mass is at a distance d=4l from the given (vertical) rotation axis. Using the parallel axis theorem the moment of inertia of one half–rod about the given axis is
Ihalf=Icm(half)+(2m)d2=96ml2+2m(4l)2=96ml2+2m⋅16l2.Since
2m⋅16l2=32ml2,we have
Ihalf=96ml2+32ml2=96ml2+963ml2=964ml2=24ml2.There are two such halves so the total moment of inertia is
Itotal=2Ihalf=2(24ml2)=12ml2.But by definition the original rod’s moment of inertia is
α=12ml2.Thus, we find
Itotal=α.The answer is that the moment of inertia of the new arrangement is the same as that of the original rod.
Explanation (minimal):
-
For a rod of mass m and length l, I=121ml2=α.
-
Each half–rod (mass m/2, length l/2) has centre‐of–mass inertia =121(m/2)(l/2)2=96ml2.
-
Using the parallel axis theorem (with d = l/4): extra term =2m(l/4)2=32ml2.
-
Thus, one half–rod’s moment =96ml2+32ml2=24ml2.
-
Two halves: 224ml2=12ml2=α.
The moment of inertia of the new arrangement equals α.
