Question
Question: The magnetic field at the centre of the circular coil of radius 1 cm and carrying current of 4 A is ...
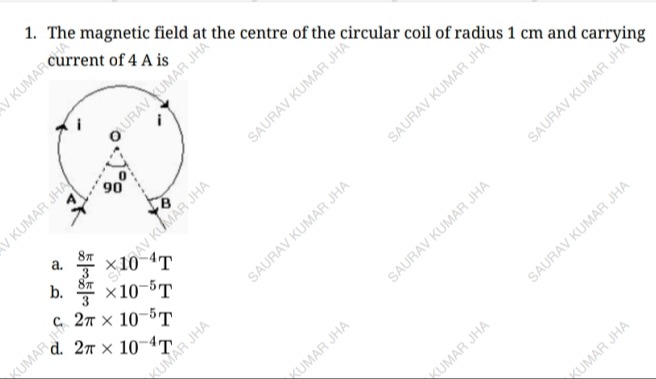
The magnetic field at the centre of the circular coil of radius 1 cm and carrying current of 4 A is
38π×10−4T
38π×10−5T
2π×10−5T
2π×10−4T
2π×10−5T
Solution
The problem asks for the magnetic field at the center of a circular coil. However, the figure shows a circular arc, not a full coil. The current 'i' is shown flowing along the arc.
Given values: Radius of the circular arc, R=1 cm=1×10−2 m. Current flowing through the arc, I=4 A.
From the figure, an angle of 90∘ is marked between the radii OA and OB.
The angle explicitly marked in the diagram is 90∘. So, the angle subtended by the current-carrying arc at the center is θ=90∘. In radians, θ=90∘×180∘π=2π radians.
Using the formula for the magnetic field at the center of a circular arc: B=4πRμ0Iθ Substituting the values: B=4π×(1×10−2 m)(4π×10−7 T m/A)×(4 A)×2π B=10−210−7×4×2π B=4×10−5×2π B=2π×10−5 T
This result matches option (c). The straight segments OA and OB do not contribute to the magnetic field at O because the point O lies on the line of these segments.
