Question

The function $f: R \rightarrow \left[-\frac{1}{2}, \frac{1}{2}\right]$ defined as $f(x) = \frac{x}{1+x^2}$, is :

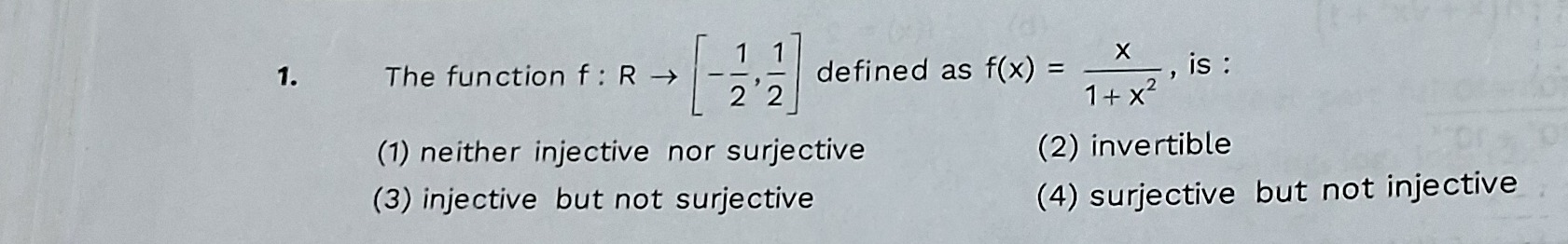
• A. neither injective nor surjective
• B. invertible
• C. injective but not surjective
• D. surjective but not injective

Answer 1

Answer: (D)

surjective but not injective

Answer 2

To check if $f$ is injective (one-one), we assume $f(x_1) = f(x_2)$ for $x_1, x_2 \in R$ and check if this implies $x_1 = x_2$.

$f(x_1) = f(x_2) \implies \frac{x_1}{1+x_1^2} = \frac{x_2}{1+x_2^2}$

$x_1(1+x_2^2) = x_2(1+x_1^2)$

$x_1 + x_1 x_2^2 = x_2 + x_2 x_1^2$

$x_1 - x_2 = x_2 x_1^2 - x_1 x_2^2$

$x_1 - x_2 = x_1 x_2 (x_1 - x_2)$

$(x_1 - x_2) - x_1 x_2 (x_1 - x_2) = 0$

$(x_1 - x_2)(1 - x_1 x_2) = 0$

This equation holds if $x_1 - x_2 = 0$ (i.e., $x_1 = x_2$) or if $1 - x_1 x_2 = 0$ (i.e., $x_1 x_2 = 1$).

Since $f(x_1) = f(x_2)$ can be true even when $x_1 \neq x_2$ (for example, if $x_1 x_2 = 1$ and $x_1 \neq x_2$, like $x_1 = 2$ and $x_2 = 1/2$, where $f(2) = \frac{2}{1+4} = \frac{2}{5}$ and $f(1/2) = \frac{1/2}{1+1/4} = \frac{1/2}{5/4} = \frac{2}{5}$), the function is not injective.

To check if $f$ is surjective (onto), we need to determine if the range of the function is equal to the codomain $\left[-\frac{1}{2}, \frac{1}{2}\right]$.

Let $y$ be in the range of $f$. Then there exists $x \in R$ such that $f(x) = y$.

$y = \frac{x}{1+x^2}$

$y(1+x^2) = x$

$y + yx^2 = x$

$yx^2 - x + y = 0$

This is a quadratic equation in $x$. For $x$ to be a real number, the discriminant must be non-negative.

The discriminant is $\Delta = (-1)^2 - 4(y)(y) = 1 - 4y^2$.

For real solutions for $x$, we must have $\Delta \ge 0$.

$1 - 4y^2 \ge 0$

$1 \ge 4y^2$

$y^2 \le \frac{1}{4}$

Taking the square root of both sides, we get $|y| \le \frac{1}{2}$, which means $-\frac{1}{2} \le y \le \frac{1}{2}$.

This shows that the range of the function is $\left[-\frac{1}{2}, \frac{1}{2}\right]$.

The codomain of the function is given as $\left[-\frac{1}{2}, \frac{1}{2}\right]$.

Since the range of the function is equal to its codomain, the function is surjective.

Thus, the function $f(x) = \frac{x}{1+x^2}$ is not injective but is surjective.