Question
Question: The degree of the differential equation $y_2^{3/2}-y_1^{1/2}-4=0$ is:...
The degree of the differential equation y23/2−y11/2−4=0 is:
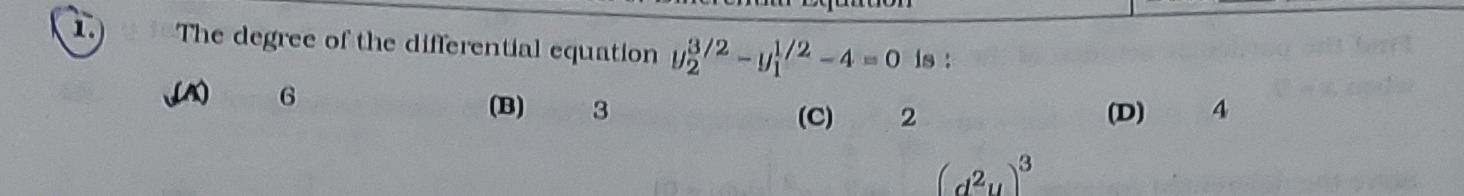
6
3
2
4
6
Solution
To find the degree of a differential equation, we first need to ensure that the equation is a polynomial in terms of its derivatives. This means eliminating any fractional powers or radicals involving the derivatives.
The given differential equation is: y23/2−y11/2−4=0
Here, y1=dxdy and y2=dx2d2y.
-
Isolate the terms with fractional powers: y23/2=y11/2+4
-
Square both sides to eliminate the fractional powers: (y23/2)2=(y11/2+4)2 y23=y1+8y11/2+16
-
Isolate the remaining term with a fractional power: y23−y1−16=8y11/2
-
Square both sides again to eliminate the remaining fractional power: (y23−y1−16)2=(8y11/2)2 (y23−y1−16)2=64y1
Now, the differential equation is expressed as a polynomial in its derivatives (y1 and y2). The highest derivative is y2=dx2d2y, so the order is 2.
The degree of the differential equation is the power of the highest order derivative after the equation has been made free from radicals and fractional powers. In the equation (y23−y1−16)2=64y1, the highest order derivative is y2. When we expand the left side, the term involving y2 with the highest power will be from (y23)2, which simplifies to y26. The power of the highest order derivative (y2) is 6.
Therefore, the degree of the differential equation is 6.
