Question
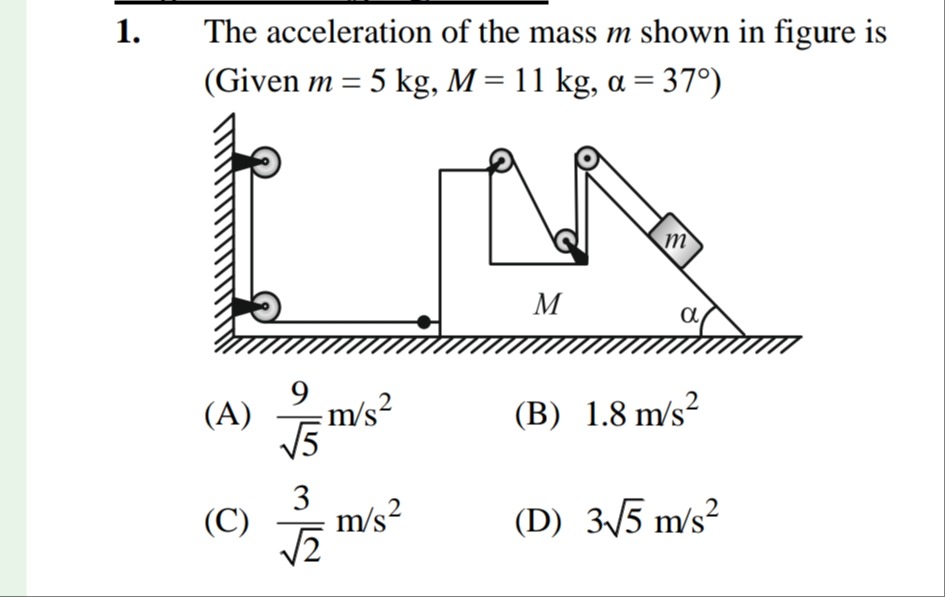
Question: The acceleration of the mass *m* shown in figure is (Given *m* = 5 kg, *M* = 11 kg, α = 37°)...
The acceleration of the mass m shown in figure is (Given m = 5 kg, M = 11 kg, α = 37°)
59 m/s²
1.8 m/s²
23 m/s²
3√5 m/s²
1.8 m/s²
Solution
-
Kinematic Relation: Let vM be the horizontal velocity of mass M and the movable pulley to the right, and vm be the velocity of mass m down the incline. By analyzing the pulley system, specifically the movable pulley connected to M, we find that the velocity of the string segment pulling M is twice the velocity of mass m along the incline. This leads to the kinematic relation vm=2vM. Consequently, the accelerations are related by am=2aM. Let aM=a, so am=2a.
-
Force Equations:
- For mass m on the incline, the forces are gravity component down the incline (mgsinα) and tension T pulling it up the incline. Applying Newton's second law: mgsinα−T=mam=m(2a) (Equation 1)
- For mass M and the movable pulley system, the movable pulley is pulled by two segments of the string, each with tension T. Applying Newton's second law to mass M: 2T=MaM=Ma (Equation 2)
-
Solving for Acceleration:
- From Equation 2, we get T=2Ma.
- Substitute this expression for T into Equation 1: mgsinα−2Ma=2ma
- Rearrange to solve for a: mgsinα=2ma+2Ma mgsinα=a(2m+2M) mgsinα=a(24m+M) a=4m+M2mgsinα
-
Numerical Calculation:
- Given values: m=5 kg, M=11 kg, α=37∘.
- Using standard approximations for JEE/NEET: g≈10 m/s² and sin37∘≈0.6.
- Substitute these values into the formula for a: a=4×5+112×5×10×0.6=3160 m/s²
- This value is approximately 1.935 m/s².
-
Comparing with Options:
- (A) 59≈4.02 m/s²
- (B) 1.8 m/s²
- (C) 23≈2.12 m/s²
- (D) 35≈6.71 m/s²
The calculated value of a=3160≈1.935 m/s² is closest to option (B) 1.8 m/s². If we use g=9.8 m/s² and sin37∘≈0.6: a=312×5×9.8×0.6=3158.8≈1.897 m/s². This value is also closest to 1.8 m/s². Therefore, option (B) is the most appropriate answer.
