Question
Question: Suppose a and b are rational and $\alpha$, $\beta$ be the roots of $x^2+2ax+b=0$, then the equation ...
Suppose a and b are rational and α, β be the roots of x2+2ax+b=0, then the equation with rational coefficients on of whose roots is α+β+α2+β2 is
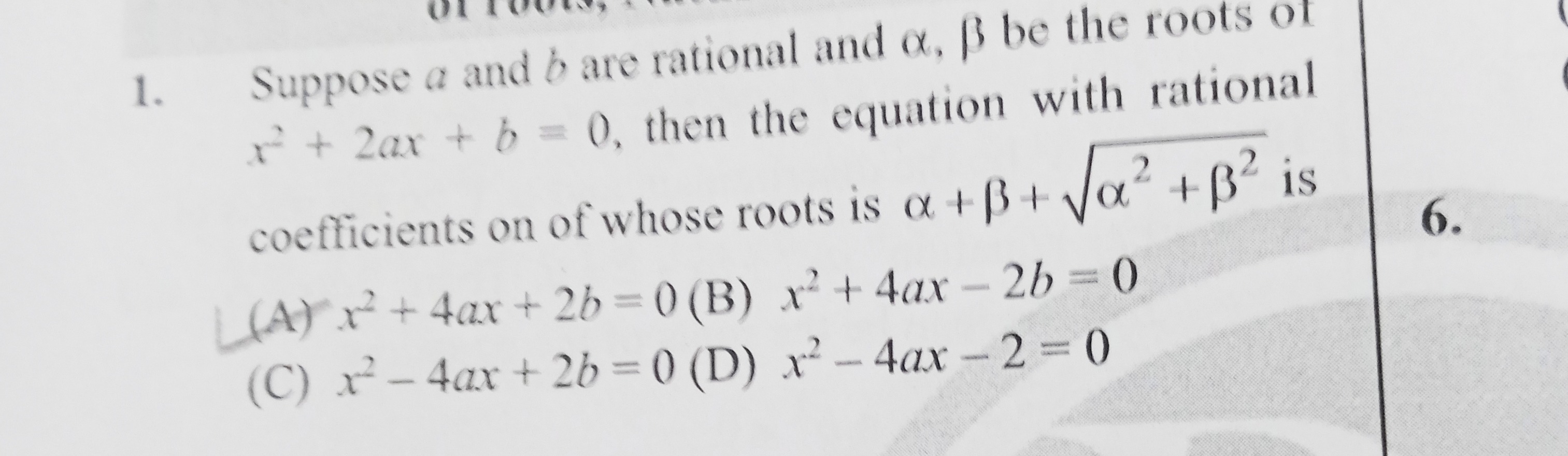
x2+4ax+2b=0
x2+4ax−2b=0
x2−4ax+2b=0
x2−4ax−2=0
x^2+4ax+2b=0
Solution
The given quadratic equation is x2+2ax+b=0.
Let its roots be α and β.
According to Vieta's formulas:
Sum of roots: α+β=−2a
Product of roots: αβ=b
We are given that a and b are rational.
We need to find an equation with rational coefficients, one of whose roots is γ=α+β+α2+β2.
First, let's simplify the term α2+β2:
We know that α2+β2=(α+β)2−2αβ.
Substitute the values of α+β and αβ:
α2+β2=(−2a)2−2(b)
α2+β2=4a2−2b
Now substitute this back into the expression for γ:
γ=(α+β)+4a2−2b
γ=−2a+4a2−2b
Let this root be X1=−2a+4a2−2b.
Since a and b are rational, −2a is rational.
For a quadratic equation to have rational coefficients, if one root is of the form p+q (where p is rational and q is irrational), then the other root must be its conjugate, p−q. If q is rational, then both roots are rational, and the rule still holds.
So, let the other root be X2=−2a−4a2−2b.
Now, we form the quadratic equation x2−(X1+X2)x+X1X2=0.
Calculate the sum of the roots (X1+X2):
X1+X2=(−2a+4a2−2b)+(−2a−4a2−2b)
X1+X2=−2a−2a+4a2−2b−4a2−2b
X1+X2=−4a
Calculate the product of the roots (X1X2):
X1X2=(−2a+4a2−2b)(−2a−4a2−2b)
This is in the form (A+B)(A−B)=A2−B2, where A=−2a and B=4a2−2b.
X1X2=(−2a)2−(4a2−2b)2
X1X2=4a2−(4a2−2b)
X1X2=4a2−4a2+2b
X1X2=2b
Substitute the sum and product of roots into the quadratic equation formula:
x2−(−4a)x+(2b)=0
x2+4ax+2b=0
All coefficients (1, 4a, 2b) are rational since a and b are rational.
Comparing this equation with the given options:
(A) x2+4ax+2b=0
(B) x2+4ax−2b=0
(C) x2−4ax+2b=0
(D) x2−4ax−2=0
The derived equation matches option (A).
The final answer is \boxed{\text{x^2+4ax+2b=0}}.
Explanation of the solution:
- Identify Given Information: The roots α,β of x2+2ax+b=0 are related by Vieta's formulas: α+β=−2a and αβ=b. a,b are rational.
- Simplify the Target Root: The desired root is γ=α+β+α2+β2. Use the identity α2+β2=(α+β)2−2αβ to express γ in terms of a and b. This gives γ=−2a+4a2−2b.
- Form the Conjugate Root: Since the coefficients of the new quadratic equation must be rational, if one root is p+q (where p is rational and q might be irrational), the other root must be its conjugate, p−q. So, the other root is −2a−4a2−2b.
- Calculate Sum and Product of New Roots:
- Sum: (−2a+4a2−2b)+(−2a−4a2−2b)=−4a.
- Product: (−2a+4a2−2b)(−2a−4a2−2b)=(−2a)2−(4a2−2b)=4a2−4a2+2b=2b.
- Construct the Equation: Use the general form x2−(sum of roots)x+(product of roots)=0. Substituting the calculated values: x2−(−4a)x+2b=0, which simplifies to x2+4ax+2b=0.
