Solveeit Logo
Login

Question

Question: Let $z_1$ and $z_2$ be two complex numbers satisfying $|z_1|=9$ and $|z_2-3-4i|=4$. Then the minimum...

Let z1z_1 and z2z_2 be two complex numbers satisfying ∣z1∣=9|z_1|=9 and ∣z2−3−4i∣=4|z_2-3-4i|=4. Then the minimum value of ∣z1−z2∣|z_1-z_2| is

A

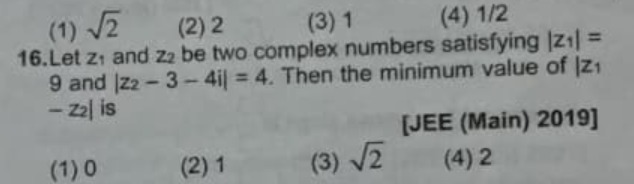
0

B

1

C

2\sqrt{2}

D

2

Answer

0

Explanation

Solution

The condition ∣z1∣=9|z_1|=9 implies that z1z_1 lies on a circle centered at the origin (0,0)(0,0) with radius r1=9r_1=9. The condition ∣z2−3−4i∣=4|z_2-3-4i|=4 implies that z2z_2 lies on a circle centered at 3+4i3+4i with radius r2=4r_2=4.

The distance between the centers of these two circles is d=∣0−(3+4i)∣=∣−(3+4i)∣=(−3)2+(−4)2=9+16=25=5d = |0 - (3+4i)| = |-(3+4i)| = \sqrt{(-3)^2 + (-4)^2} = \sqrt{9+16} = \sqrt{25} = 5.

We compare the distance between the centers dd with the difference of the radii ∣r1−r2∣|r_1 - r_2|. ∣r1−r2∣=∣9−4∣=5|r_1 - r_2| = |9 - 4| = 5.

Since d=∣r1−r2∣d = |r_1 - r_2|, the two circles touch internally. When two circles touch internally, the minimum distance between any point on the first circle and any point on the second circle is 0. This occurs at the point of tangency.