Question

$\sin^6 x + \cos^6 x = 1-\frac{6}{6}$

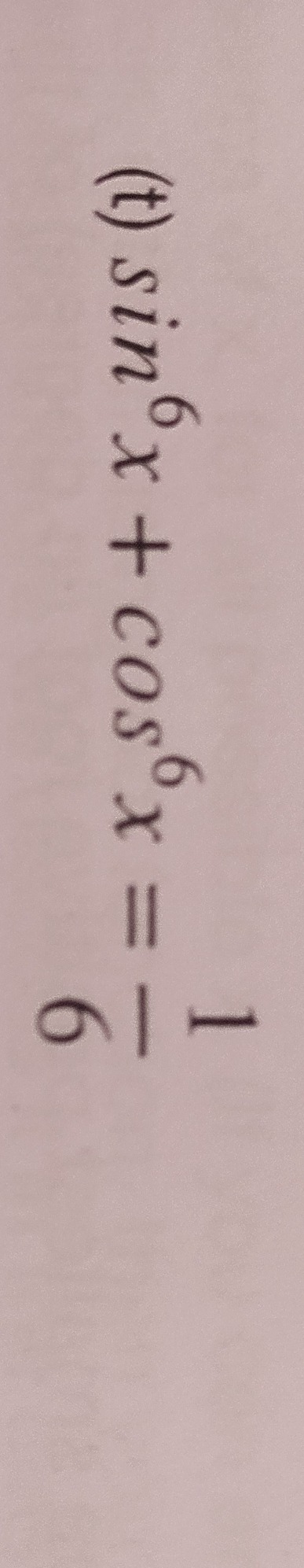
Answer 1

The equation has no real solutions. The solution set is $\emptyset$.

Answer 2

The equation simplifies to $\sin^6 x + \cos^6 x = 0$. For real $x$, $\sin^6 x \ge 0$ and $\cos^6 x \ge 0$. The sum is zero only if $\sin^6 x = 0$ and $\cos^6 x = 0$, which means $\sin x = 0$ and $\cos x = 0$. This contradicts the identity $\sin^2 x + \cos^2 x = 1$. Thus, no real solutions exist.