Question

Range of the function $f(x) = \log_2(2 - \log_5(16\sin^2x + 1))$ is :

Answer 1

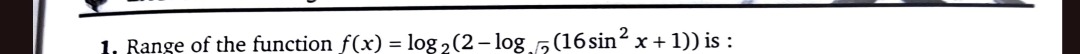
$[\log_2(2 - \log_5(17)), 1]$

Answer 2

Let the given function be $f(x) = \log_2(2 - \log_5(16\sin^2x + 1))$.

For the function to be defined, the following conditions must be met:

1. The argument of the inner logarithm must be positive: $16\sin^2x + 1 > 0$.
   Since $0 \le \sin^2x \le 1$ for any real $x$, we have $16\sin^2x \ge 0$. Thus, $16\sin^2x + 1 \ge 1$. This condition is always satisfied for all real $x$.

2. The argument of the outer logarithm must be positive: $2 - \log_5(16\sin^2x + 1) > 0$.
   $2 > \log_5(16\sin^2x + 1)$.
   Since the base of the logarithm is 5, which is greater than 1, the inequality can be rewritten as:
   $5^2 > 16\sin^2x + 1$
   $25 > 16\sin^2x + 1$
   $24 > 16\sin^2x$
   $\sin^2x < \frac{24}{16} = \frac{3}{2}$.
   Since the range of $\sin^2x$ is $[0, 1]$ for any real $x$, the condition $\sin^2x < \frac{3}{2}$ is always satisfied because $1 < \frac{3}{2}$.
   Thus, the domain of the function $f(x)$ is all real numbers $x$.

Now, let's determine the range of the function.
We know that for any real $x$, $0 \le \sin^2x \le 1$.
Let $u = 16\sin^2x + 1$.
Multiplying the inequality $0 \le \sin^2x \le 1$ by 16, we get $0 \le 16\sin^2x \le 16$.
Adding 1 to all parts, we get $0 + 1 \le 16\sin^2x + 1 \le 16 + 1$, which means $1 \le u \le 17$.
The range of $u = 16\sin^2x + 1$ is $[1, 17]$.

Next, consider the term $\log_5(u) = \log_5(16\sin^2x + 1)$.
Since $u \in [1, 17]$ and the base of the logarithm (5) is greater than 1, $\log_5(u)$ is an increasing function.
The minimum value of $\log_5(u)$ occurs when $u=1$, which is $\log_5(1) = 0$.
The maximum value of $\log_5(u)$ occurs when $u=17$, which is $\log_5(17)$.
The range of $\log_5(16\sin^2x + 1)$ is $[\log_5(1), \log_5(17)] = [0, \log_5(17)]$.

Now, consider the argument of the outer logarithm, $w = 2 - \log_5(16\sin^2x + 1)$.
Let $v = \log_5(16\sin^2x + 1)$. The range of $v$ is $[0, \log_5(17)]$.
The expression is $2 - v$.
The minimum value of $2 - v$ occurs when $v$ is maximum: $2 - \log_5(17)$.
The maximum value of $2 - v$ occurs when $v$ is minimum: $2 - 0 = 2$.
The range of $w = 2 - \log_5(16\sin^2x + 1)$ is $[2 - \log_5(17), 2]$.
We need to verify that this range is positive, as required by the domain of $\log_2$.
Since $5^1 = 5$ and $5^2 = 25$, we know that $1 < \log_5(17) < 2$.
Therefore, $2 - 2 < 2 - \log_5(17) < 2 - 1$, which means $0 < 2 - \log_5(17) < 1$.
The range $[2 - \log_5(17), 2]$ is indeed a subset of $(0, \infty)$.

Finally, consider the function $f(x) = \log_2(w) = \log_2(2 - \log_5(16\sin^2x + 1))$.
Since $w \in [2 - \log_5(17), 2]$ and the base of the logarithm (2) is greater than 1, $\log_2(w)$ is an increasing function.
The minimum value of $\log_2(w)$ occurs when $w$ is minimum: $\log_2(2 - \log_5(17))$.
The maximum value of $\log_2(w)$ occurs when $w$ is maximum: $\log_2(2) = 1$.
The range of $f(x)$ is $[\log_2(2 - \log_5(17)), 1]$.