Question

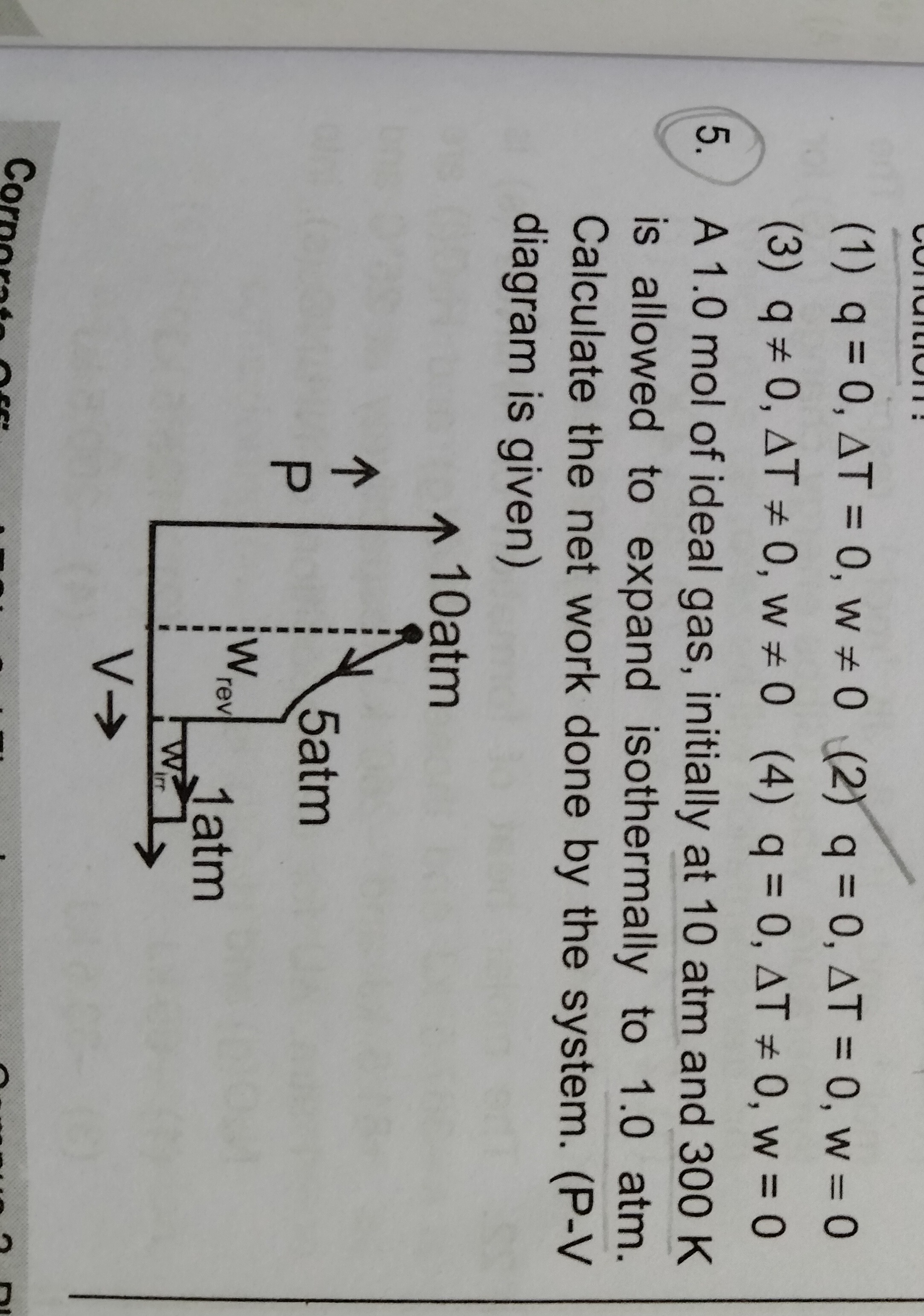
A 1.0 mol of ideal gas, initially at 10 atm and 300 K is allowed to expand isothermally to 1.0 atm. Calculate the net work done by the system. (P-V diagram is given)

• A. q = 0, ΔT = 0, w ≠ 0
• B. q = 0, ΔT = 0, w = 0
• C. q ≠ 0, ΔT ≠ 0, w ≠ 0
• D. q = 0, ΔT ≠ 0, w = 0

Answer 1

(1)

Answer 2

The process described is an isothermal expansion of an ideal gas. For an isothermal process, the temperature remains constant, so $\Delta T = 0$. For an ideal gas, internal energy ($U$) is a function of temperature only. Therefore, for an isothermal process, $\Delta U = 0$. According to the First Law of Thermodynamics, $\Delta U = q + w$, where $q$ is heat added to the system and $w$ is work done on the system. Since $\Delta U = 0$, we have $q + w = 0$, which means $q = -w$.

During an expansion, the volume increases, and work is done by the system. Work done by the system is positive ($W_{by} > 0$). The work done on the system ($w$) is the negative of the work done by the system ($w = -W_{by}$). Thus, during expansion, $w < 0$.

Since $q = -w$ and $w < 0$, it implies that $q > 0$. This means heat is absorbed by the system to maintain a constant temperature during expansion.

Therefore, for an isothermal expansion of an ideal gas, the conditions are $\Delta T = 0$, $q > 0$, and $w < 0$.

Let's examine the options: (1) $q = 0, \Delta T = 0, w \neq 0$: This option correctly states $\Delta T = 0$ and $w \neq 0$ (since work is done during expansion). However, it incorrectly states $q = 0$. (2) $q = 0, \Delta T = 0, w = 0$: This implies no change, which is incorrect for an expansion. (3) $q \neq 0, \Delta T \neq 0, w \neq 0$: This option incorrectly states $\Delta T \neq 0$. (4) $q = 0, \Delta T \neq 0, w = 0$: This option incorrectly states $\Delta T \neq 0$.

Option (1) is the closest to the correct description of an isothermal expansion, despite the error in the condition for $q$. If the question is asking to select the best description among the given options, option (1) is the most appropriate choice as it correctly identifies the isothermal nature ($\Delta T = 0$) and the occurrence of work ($w \neq 0$).

The work done by the system during an isothermal expansion is calculated using the formula: $W_{by} = nRT \ln\left(\frac{P_1}{P_2}\right)$ Given: $n = 1.0$ mol $R = 8.314$ J/mol·K $T = 300$ K $P_1 = 10$ atm $P_2 = 1.0$ atm

$W_{by} = (1.0 \text{ mol}) \times (8.314 \text{ J/mol·K}) \times (300 \text{ K}) \times \ln\left(\frac{10 \text{ atm}}{1.0 \text{ atm}}\right)$ $W_{by} = 2494.2 \times \ln(10)$ $W_{by} \approx 2494.2 \times 2.3026$ $W_{by} \approx 5743.6$ J

If using $R = 0.0821$ L·atm/mol·K: $W_{by} = (1.0 \text{ mol}) \times (0.0821 \text{ L·atm/mol·K}) \times (300 \text{ K}) \times \ln\left(\frac{10 \text{ atm}}{1.0 \text{ atm}}\right)$ $W_{by} = 24.63 \times \ln(10)$ $W_{by} \approx 24.63 \times 2.3026$ $W_{by} \approx 56.74$ L·atm

Since the options provided are descriptive and not numerical values of work, and option (1) best describes the conditions of an isothermal process with work being done, it is considered the correct answer in the context of selecting the most fitting description.