Question

1. One end of a rope is fixed at a point on the ceiling the other end is held close to the first end so that the rope folded. The second end is released from this position. Find the speed at which the fold at F is descending at the instant the free end of the rope is going down at speed v.

Answer 1

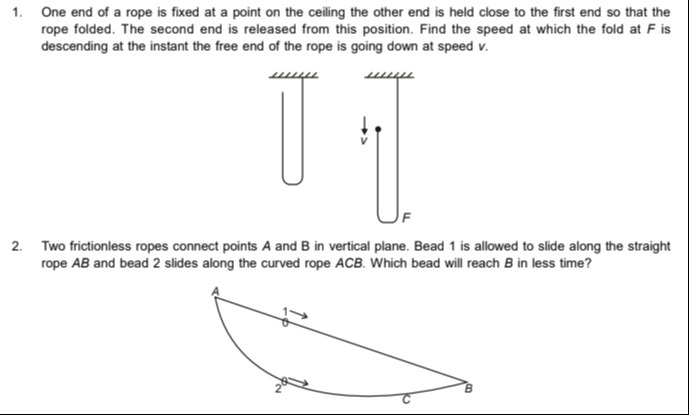
The speed at which the fold at F is descending is v/2.

Answer 2

Let $y_F$ be the vertical position of the fold F from the fixed point on the ceiling, and $y_E$ be the vertical position of the free end E from the fixed point. Both positions are measured downwards from the ceiling.

The length of the rope from the fixed point to the fold is $y_F$. Since the rope is folded at F, the segment of the rope from F to the free end E has length $y_E - y_F$.

The total length of the rope is given by: $L = y_F + (y_E - y_F) = y_E$

Since the length of the rope is constant, we have: $\frac{dL}{dt} = 0$

Differentiating the equation with respect to time: $\frac{d}{dt}(2y_F - y_E) = 0$ $2\frac{dy_F}{dt} - \frac{dy_E}{dt} = 0$

Given that the free end of the rope is going down at speed v, we have: $\frac{dy_E}{dt} = v$

Therefore, $2\frac{dy_F}{dt} - v = 0$ $2\frac{dy_F}{dt} = v$ $\frac{dy_F}{dt} = \frac{v}{2}$

Thus, the speed at which the fold at F is descending is $\frac{v}{2}$.