Solveeit Logo
Login

Question

Question: 1 mol of ideal gas is expanded from (10 atm, 10 L) to (2 atm, 50 L) isothermally. Calculate: q, $\De...

1 mol of ideal gas is expanded from (10 atm, 10 L) to (2 atm, 50 L) isothermally. Calculate: q, ΔU\Delta U, ΔH\Delta H, W.

A

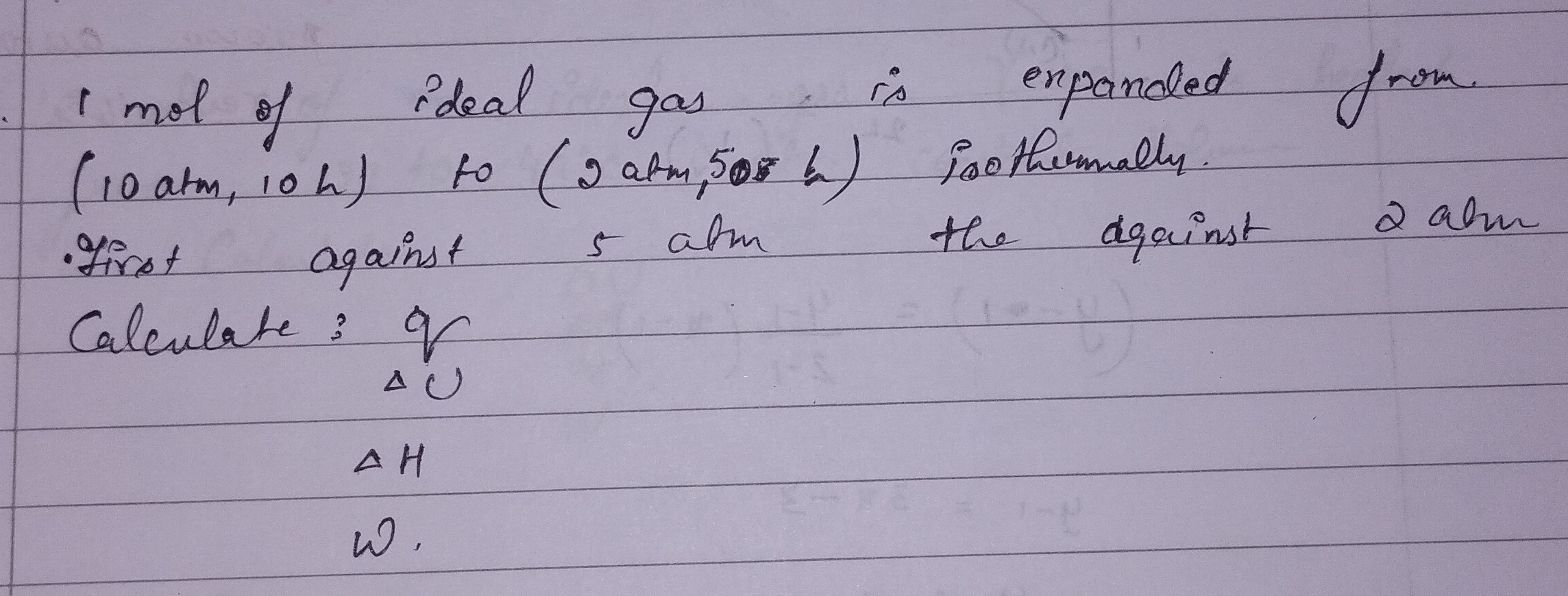
q = 11.15 kJ, ΔU\Delta U = 0 kJ, ΔH\Delta H = 0 kJ, W = -11.15 kJ

B

q = 0 kJ, ΔU\Delta U = 11.15 kJ, ΔH\Delta H = 0 kJ, W = -11.15 kJ

C

q = 11.15 kJ, ΔU\Delta U = 0 kJ, ΔH\Delta H = 11.15 kJ, W = 0 kJ

D

q = 0 kJ, ΔU\Delta U = 0 kJ, ΔH\Delta H = 0 kJ, W = -11.15 kJ

Answer

q = 11.15 kJ, ΔU\Delta U = 0 kJ, ΔH\Delta H = 0 kJ, W = -11.15 kJ

Explanation

Solution

For an isothermal process of an ideal gas, ΔU=0\Delta U = 0 and ΔH=0\Delta H = 0. The work done in an isothermal expansion is given by W=−nRTln⁡(V2V1)W = -nRT \ln(\frac{V_2}{V_1}). Given: n=1n=1 mol, TT is constant, P1=10P_1 = 10 atm, V1=10V_1 = 10 L, P2=2P_2 = 2 atm. Using Boyle's Law for an isothermal process: P1V1=P2V2P_1V_1 = P_2V_2. 10 atm×10 L=2 atm×V210 \text{ atm} \times 10 \text{ L} = 2 \text{ atm} \times V_2 V2=1002=50V_2 = \frac{100}{2} = 50 L.

The work done is W=−PextΔVW = -P_{ext} \Delta V. The problem states expansion against 5 atm then against 2 atm, indicating an irreversible, multi-stage expansion.

Stage 1: Expansion from V1=10V_1 = 10 L to an intermediate volume VintV_{int} against Pext,1=5P_{ext,1} = 5 atm. The gas pressure drops until it equals the external pressure. Using Boyle's Law for the gas itself: P1V1=Pgas,intVintP_1V_1 = P_{gas,int}V_{int} 10 atm×10 L=5 atm×Vint10 \text{ atm} \times 10 \text{ L} = 5 \text{ atm} \times V_{int} Vint=1005=20V_{int} = \frac{100}{5} = 20 L. Work done in Stage 1: W1=−Pext,1(Vint−V1)=−5 atm×(20 L−10 L)=−5 atm×10 L=−50W_1 = -P_{ext,1} (V_{int} - V_1) = -5 \text{ atm} \times (20 \text{ L} - 10 \text{ L}) = -5 \text{ atm} \times 10 \text{ L} = -50 atm L.

Stage 2: Expansion from Vint=20V_{int} = 20 L to V2=50V_2 = 50 L against Pext,2=2P_{ext,2} = 2 atm. Work done in Stage 2: W2=−Pext,2(V2−Vint)=−2 atm×(50 L−20 L)=−2 atm×30 L=−60W_2 = -P_{ext,2} (V_2 - V_{int}) = -2 \text{ atm} \times (50 \text{ L} - 20 \text{ L}) = -2 \text{ atm} \times 30 \text{ L} = -60 atm L.

Total Work: W=W1+W2=−50 atm L+(−60 atm L)=−110W = W_1 + W_2 = -50 \text{ atm L} + (-60 \text{ atm L}) = -110 atm L.

Convert work to Joules: 1 atm L=101.325 J1 \text{ atm L} = 101.325 \text{ J}. W=−110×101.325 J=−11145.75 J≈−11.15 kJW = -110 \times 101.325 \text{ J} = -11145.75 \text{ J} \approx -11.15 \text{ kJ}.

From the First Law of Thermodynamics, ΔU=q+W\Delta U = q + W. Since ΔU=0\Delta U = 0 for an isothermal process of an ideal gas, 0=q+W0 = q + W, so q=−Wq = -W. q=−(−110 atm L)=110 atm Lq = -(-110 \text{ atm L}) = 110 \text{ atm L}. q=110×101.325 J=11145.75 J≈11.15 kJq = 110 \times 101.325 \text{ J} = 11145.75 \text{ J} \approx 11.15 \text{ kJ}.

Therefore: q≈11.15 kJq \approx 11.15 \text{ kJ} ΔU=0 kJ\Delta U = 0 \text{ kJ} ΔH=0 kJ\Delta H = 0 \text{ kJ} W≈−11.15 kJW \approx -11.15 \text{ kJ}