Question

Magnetic field is increasing in a circular region of radius 2 m at a rate 30 Tesla/sec. O is the centre of circular region which is taken as origin. A smooth tunnel is formed in this plane which is represented as $y = \pm (\sqrt{3})x^2$. A charge particle q enters into the tunnel at M with a kinetic energy $E_1$ and leaves the tunnel at N with kinetic energy $E_2$. Mark the correct statement.

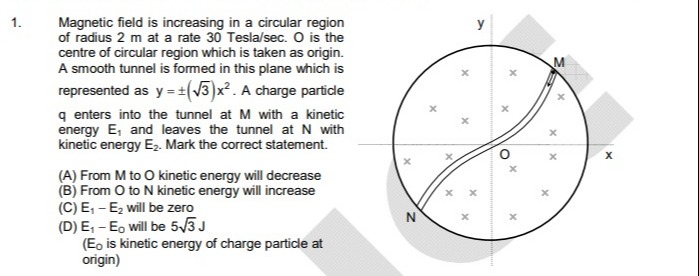
• A. From M to O kinetic energy will decrease
• B. From O to N kinetic energy will increase
• C. $E_1 - E_2$ will be zero
• D. $E_1 - E_0$ will be $5\sqrt{3}$ J ($E_0$ is kinetic energy of charge particle at origin)

Answer 1

Answer: (C)

C

Answer 2

The magnetic field is increasing in a circular region of radius 2 m at a rate $dB/dt = 30 \, \text{T/s}$. The induced electric field at a distance $r$ from the center is given by $E = \frac{1}{2} r \frac{dB}{dt}$. The direction of the induced electric field is tangential and counter-clockwise. In Cartesian coordinates, $\vec{E} = \frac{1}{2} \frac{dB}{dt} (-y, x) = 15 (-y, x)$.

The tunnel is represented by $y = \pm \sqrt{3}x^2$. The particle enters at M and leaves at N. The tunnel intersects the circle $x^2+y^2 = 2^2 = 4$. For the upper branch $y = \sqrt{3}x^2$, $x^2 + (\sqrt{3}x^2)^2 = 4 \implies x^2 + 3x^4 = 4 \implies 3x^4 + x^2 - 4 = 0$. Let $u=x^2$, then $3u^2 + u - 4 = 0 \implies (3u+4)(u-1) = 0$. Since $u=x^2 \ge 0$, $u=1$, so $x^2=1$, $x = \pm 1$. For $x=1$, $y = \sqrt{3}(1)^2 = \sqrt{3}$. So M is at $(1, \sqrt{3})$. For $x=-1$, $y = \sqrt{3}(-1)^2 = \sqrt{3}$. This point is not N. For the lower branch $y = -\sqrt{3}x^2$, $x^2 + (-\sqrt{3}x^2)^2 = 4 \implies 3x^4 + x^2 - 4 = 0$, so $x^2=1$, $x = \pm 1$. For $x=-1$, $y = -\sqrt{3}(-1)^2 = -\sqrt{3}$. So N is at $(-1, -\sqrt{3})$. The tunnel passes through the origin O $(0,0)$.

The change in kinetic energy of the charged particle is equal to the work done by the electric field: $\Delta K = W_E = q \int \vec{E} \cdot d\vec{l}$. $W_E = q \int 15 (-y \, dx + x \, dy)$.

From M to O, the path is $y = \sqrt{3}x^2$, $dy = 2\sqrt{3}x \, dx$. The integration is from $(1, \sqrt{3})$ to $(0, 0)$, i.e., from $x=1$ to $x=0$. $W_{M \to O} = 15q \int_{x=1}^{0} (-\sqrt{3}x^2 \, dx + x(2\sqrt{3}x \, dx)) = 15q \int_{1}^{0} \sqrt{3}x^2 \, dx = 15q \sqrt{3} [\frac{x^3}{3}]_{1}^{0} = 15q \sqrt{3} (0 - \frac{1}{3}) = -5\sqrt{3}q$. The change in kinetic energy from M to O is $E_0 - E_1 = W_{M \to O} = -5\sqrt{3}q$. So $E_1 - E_0 = 5\sqrt{3}q$.

From O to N, the path is $y = -\sqrt{3}x^2$, $dy = -2\sqrt{3}x \, dx$. The integration is from $(0, 0)$ to $(-1, -\sqrt{3})$, i.e., from $x=0$ to $x=-1$. $W_{O \to N} = 15q \int_{x=0}^{-1} (- (-\sqrt{3}x^2) \, dx + x(-2\sqrt{3}x \, dx)) = 15q \int_{0}^{-1} (\sqrt{3}x^2 - 2\sqrt{3}x^2) \, dx = 15q \int_{0}^{-1} (-\sqrt{3}x^2) \, dx = -15q \sqrt{3} [\frac{x^3}{3}]_{0}^{-1} = -15q \sqrt{3} (\frac{(-1)^3}{3} - 0) = -15q \sqrt{3} (-\frac{1}{3}) = 5\sqrt{3}q$. The change in kinetic energy from O to N is $E_2 - E_0 = W_{O \to N} = 5\sqrt{3}q$.

The total change in kinetic energy from M to N is $E_2 - E_1 = W_{M \to N} = W_{M \to O} + W_{O \to N} = -5\sqrt{3}q + 5\sqrt{3}q = 0$. So, $E_1 - E_2 = 0$.

Let's evaluate the options:

(A) From M to O kinetic energy will decrease. $E_0 - E_1 = -5\sqrt{3}q$. If $q > 0$, $E_0 < E_1$, so kinetic energy decreases. If $q < 0$, $E_0 > E_1$, so kinetic energy increases. This statement is not always true.

(B) From O to N kinetic energy will increase. $E_2 - E_0 = 5\sqrt{3}q$. If $q > 0$, $E_2 > E_0$, so kinetic energy increases. If $q < 0$, $E_2 < E_0$, so kinetic energy decreases. This statement is not always true.

(C) $E_1 - E_2$ will be zero. This is true as calculated above.

(D) $E_1 - E_0$ will be $5\sqrt{3}$ J. We found $E_1 - E_0 = 5\sqrt{3}q$. This statement is true only if $q=1$ C. Since the charge $q$ is not given to be 1 C, this statement is not necessarily true.

Therefore, the only correct statement is (C).