Question

$\log^2(4-x) + \log(4-x)\log(x+1/2) = 2.\log^2(x+1/2)$

Answer 1

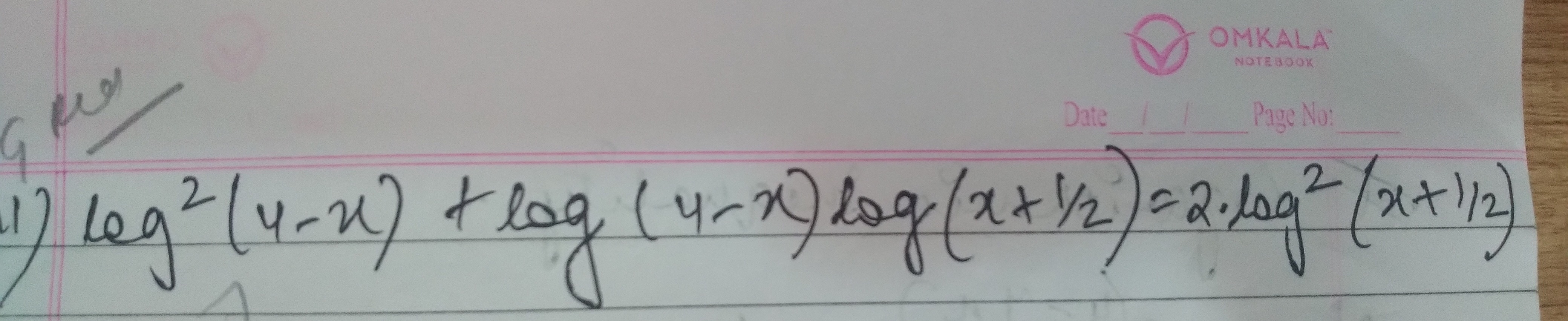
The solutions to the equation are $x = 0$, $x = \frac{7}{4}$, and $x = \frac{3 + 2\sqrt{6}}{2}$.

Answer 2

The domain of the logarithmic functions requires $4-x > 0$ and $x+1/2 > 0$, which implies $-1/2 < x < 4$.

Let $A = \log(4-x)$ and $B = \log(x+1/2)$. The equation becomes: $A^2 + AB = 2B^2$ Rearranging gives: $A^2 + AB - 2B^2 = 0$ This is a quadratic equation in terms of $A$ and $B$, which can be factored as: $(A - B)(A + 2B) = 0$ This leads to two cases:

Case 1: $A - B = 0 \implies A = B$ $\log(4-x) = \log(x+1/2)$ Since the logarithm function is one-to-one, we equate the arguments: $4-x = x+1/2$ $4 - \frac{1}{2} = 2x$ $\frac{7}{2} = 2x$ $x = \frac{7}{4}$ This value $x=7/4$ is within the domain $-1/2 < x < 4$.

Case 2: $A + 2B = 0 \implies A = -2B$ $\log(4-x) = -2\log(x+1/2)$ Using the logarithm property $n\log m = \log m^n$: $\log(4-x) = \log((x+1/2)^{-2})$ Equating the arguments: $4-x = (x+1/2)^{-2} = \frac{1}{(x+1/2)^2}$ $(4-x)(x+1/2)^2 = 1$ Expanding $(x+1/2)^2 = x^2 + x + 1/4$: $(4-x)(x^2 + x + 1/4) = 1$ $4x^2 + 4x + 1 - x^3 - x^2 - \frac{x}{4} = 1$ $-x^3 + 3x^2 + \frac{15x}{4} = 0$ Multiplying by $-4$ to clear fractions and make the leading coefficient positive: $4x^3 - 12x^2 - 15x = 0$ Factoring out $x$: $x(4x^2 - 12x - 15) = 0$ This yields $x=0$ or $4x^2 - 12x - 15 = 0$.

• For $x=0$: This value is within the domain $-1/2 < x < 4$.

• For $4x^2 - 12x - 15 = 0$: Using the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$: $x = \frac{12 \pm \sqrt{(-12)^2 - 4(4)(-15)}}{2(4)} = \frac{12 \pm \sqrt{144 + 240}}{8} = \frac{12 \pm \sqrt{384}}{8}$ Since $\sqrt{384} = \sqrt{64 \times 6} = 8\sqrt{6}$: $x = \frac{12 \pm 8\sqrt{6}}{8} = \frac{3 \pm 2\sqrt{6}}{2}$ We have two potential solutions: $x_1 = \frac{3 + 2\sqrt{6}}{2}$ and $x_2 = \frac{3 - 2\sqrt{6}}{2}$.

  • Checking $x_1 = \frac{3 + 2\sqrt{6}}{2}$: This value is approximately $3.95$, which lies within the domain $-1/2 < x < 4$.

  • Checking $x_2 = \frac{3 - 2\sqrt{6}}{2}$: This value is approximately $-0.95$, which is less than $-1/2$. Thus, it is outside the domain and is an extraneous solution.

The valid solutions are $x=0$, $x=7/4$, and $x = \frac{3 + 2\sqrt{6}}{2}$.