Question
Question: Locus of the mid points of the segments which are tangents to the ellipse $\frac{1}{2}x^2+y^2=1$ and...
Locus of the mid points of the segments which are tangents to the ellipse 21x2+y2=1 and which are intercepted between the coordinate axes is -
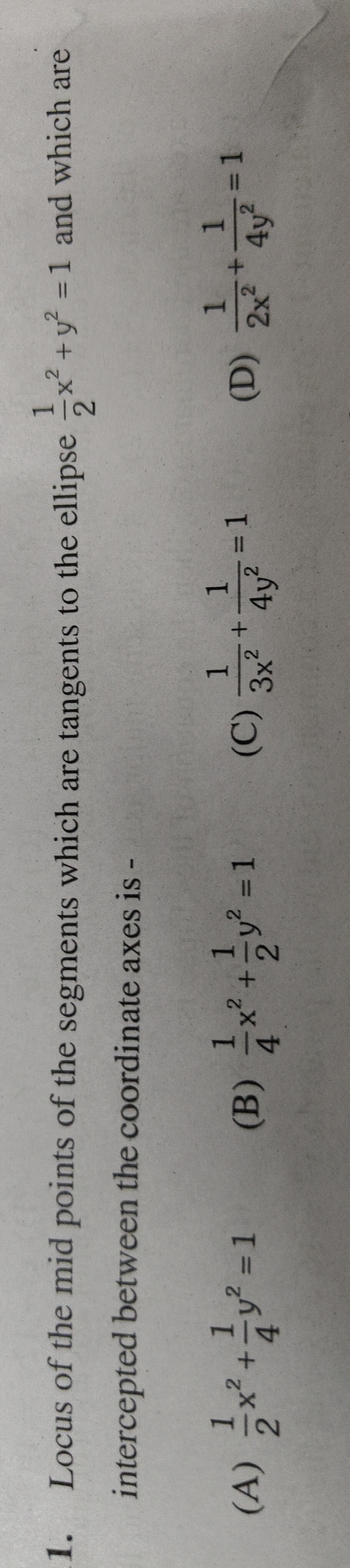
21x2+41y2=1
41x2−21y2=1
3x21+4y21=1
2x21+4y21=1
2x21+4y21=1
Solution
The equation of the given ellipse is 2x2+1y2=1. The equation of the tangent to the ellipse at a point (x0,y0) on the ellipse is 2xx0+1yy0=1. To find the x-intercept, set y=0: 2xx0=1⟹x=x02. So, the x-intercept point is P(x02,0). To find the y-intercept, set x=0: yy0=1⟹y=y01. So, the y-intercept point is Q(0,y01). The midpoint M(h,k) of the segment PQ is given by: h=2x02+0=x01 k=20+y01=2y01 From these, we get x0=h1 and y0=2k1. Since (x0,y0) lies on the ellipse, it must satisfy the ellipse equation: 2x02+y02=1 Substitute the expressions for x0 and y0: 2(1/h)2+(2k1)2=1 2h21+4k21=1 Replacing (h,k) with (x,y) to get the locus equation: 2x21+4y21=1
