Question

Let x, y ∈ R such that cosxcosy + 2siny + 2sinxcosy = 3, then find the value of tan²x + 5tan²y.

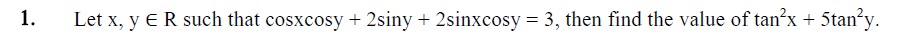
Answer 1

8

Answer 2

1. Rewrite the equation as $\cos y (\cos x+2\sin x) + 2\sin y =3$.

2. Let $A=\cos x+2\sin x$; maximum value of $A\cos y+2\sin y$ is $\sqrt{A^2+4}$ which must equal 3, forcing $A^2=5$ and $A=\sqrt{5}$.

3. Write $\cos x+2\sin x = \sqrt{5}\sin(x+\alpha)$ with $\sin\alpha=1/\sqrt{5}$, $\cos\alpha=2/\sqrt{5}$.

4. Then $\sin(x+\alpha)=1$ leading to $\tan x=2$.

5. Find $\tan y$ from $\cos y=\sqrt{5}/3$ and $\sin y=2/3$ to get $\tan y=2/\sqrt{5}$.

6. Finally, compute $\tan^2 x+5\tan^2 y=4+4=8$.