Question

Let sequence $\{a_n\}$ satisfy $a_1 = 1, a_2 = 4, a_3 = 5$ and $a_n + a_{n-1} + a_{n-2} + a_{n-3} = n^2 \forall n \ge 4$. If $\frac{\text{sum of digits of } a_{2021}}{10}$ is P then P is

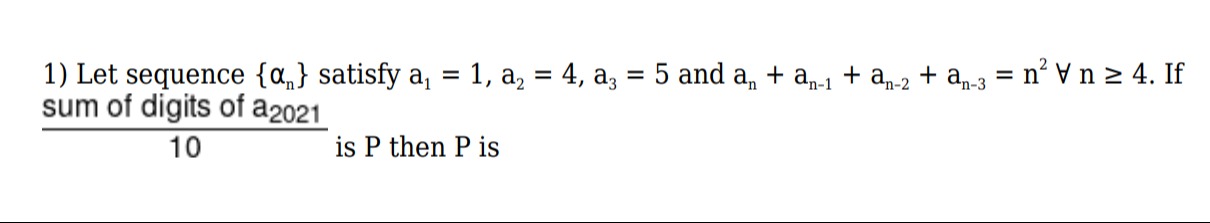
Answer 1

1.9

Answer 2

The sequence $\{a_n\}$ is defined by $a_1 = 1, a_2 = 4, a_3 = 5$ and $a_n + a_{n-1} + a_{n-2} + a_{n-3} = n^2$ for $n \ge 4$. The general solution is found to be $a_n = \frac{n^2+3n+1 - 5\cos(\frac{\pi n}{2}) - \sin(\frac{\pi n}{2})}{4}$. For $n=2021$, we have $\cos(\frac{2021\pi}{2}) = 0$ and $\sin(\frac{2021\pi}{2}) = 1$. So, $a_{2021} = \frac{2021^2 + 3(2021) + 1 - 5(0) - 1}{4} = \frac{2021(2021+3)}{4} = \frac{2021 \times 2024}{4} = 2021 \times 506 = 1022626$. The sum of the digits of $a_{2021}$ is $1+0+2+2+6+2+6 = 19$. P is given by $\frac{\text{sum of digits of } a_{2021}}{10} = \frac{19}{10} = 1.9$.