Question

Let P be (5, 3) and a point R on y = x and Q on the x-axis be such that PQ + QR + RP is minimum. Then the coordinates of Q are

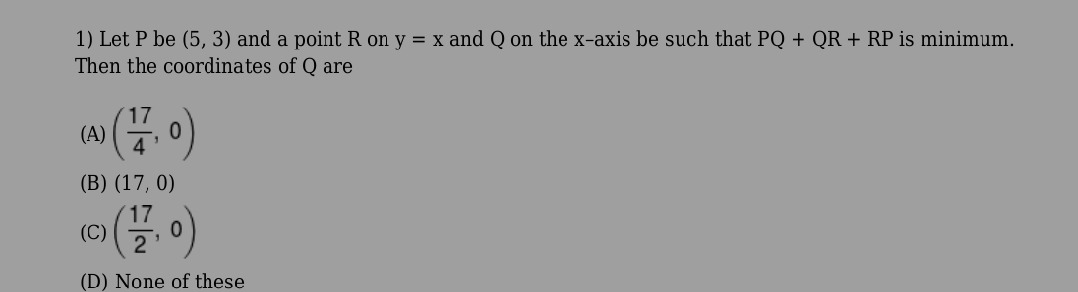
• A. ($\frac{17}{4}$, 0)
• B. (17, 0)
• C. ($\frac{17}{2}$, 0)
• D. None of these

Answer 1

Answer: (A)

($\frac{17}{4}$, 0)

Answer 2

To minimize PQ + QR + RP, we use the reflection principle. Let P = (5, 3). Reflect P across the x-axis to get P' = (5, -3). Then PQ = P'Q. Reflect P across the line y=x to get P_y = (3, 5). Then RP = RP_y. The sum becomes P'Q + QR + RP_y. This sum is minimized when P', Q, R, and P_y are collinear. The line passing through P'(5, -3) and P_y(3, 5) has the equation: Slope $m = \frac{5 - (-3)}{3 - 5} = \frac{8}{-2} = -4$. Equation: $y - 5 = -4(x - 3) \implies y = -4x + 12 + 5 \implies y = -4x + 17$. Point Q is on the x-axis, so its y-coordinate is 0. $0 = -4x + 17 \implies 4x = 17 \implies x = \frac{17}{4}$. Thus, Q is $(\frac{17}{4}, 0)$.