Question
Question: Let $\overrightarrow{x}$, $\overrightarrow{y}$ are non zero and non collinear vectors such that $(a\...
Let x, y are non zero and non collinear vectors such that (aα2+bα+c)x+(aβ2+bβ+c)y+(aγ2+bγ+c)(x×y)=0, then (a+b+c) is (where a,b,c ∈ R)
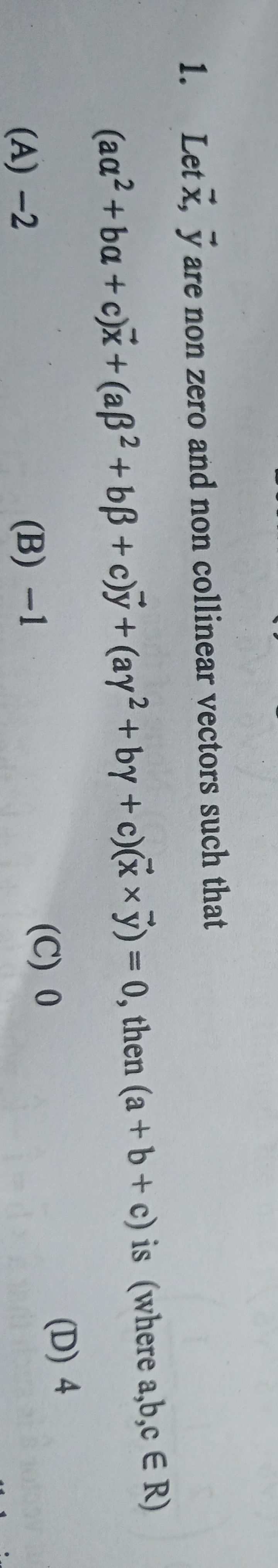
-2
-1
0
4
0
Solution
The given vector equation is a linear combination of vectors x, y, and x×y equal to the zero vector. Since x and y are non-zero and non-collinear, the set of vectors {x,y,x×y} is linearly independent. Thus, the coefficients in the linear combination must all be zero.
Let P(t)=at2+bt+c. The coefficients are P(α), P(β), and P(γ). So, we have P(α)=0, P(β)=0, and P(γ)=0. This means that α, β, and γ are roots of the polynomial equation at2+bt+c=0.
A polynomial of degree at most 2 (at2+bt+c) can have at most two distinct roots unless it is the zero polynomial (a=0,b=0,c=0). The problem asks for a unique value of a+b+c.
If α,β,γ are distinct, then the only way for them to be roots is if a=0,b=0,c=0. In this case, a+b+c=0.
If α,β,γ are not distinct, the equations P(α)=0,P(β)=0,P(γ)=0 might have non-zero solutions for a,b,c. However, the value of a+b+c=P(1) would not be uniquely determined in general (it would depend on α,γ and a if α=β=γ, or on α and a if α=β=γ).
The fact that the question asks for a unique value of a+b+c implies that the conditions must force a=b=c=0, which occurs when α,β,γ are distinct.
Assuming α,β,γ are distinct, we get a=b=c=0. Therefore, a+b+c=0+0+0=0.
