Question

Let $f: R \rightarrow (\frac{\pi}{2}, \pi]$, $f(x) = \sec^{-1}(a+2x-x^2)$ is onto function. Then the exhaustive set of values of a is

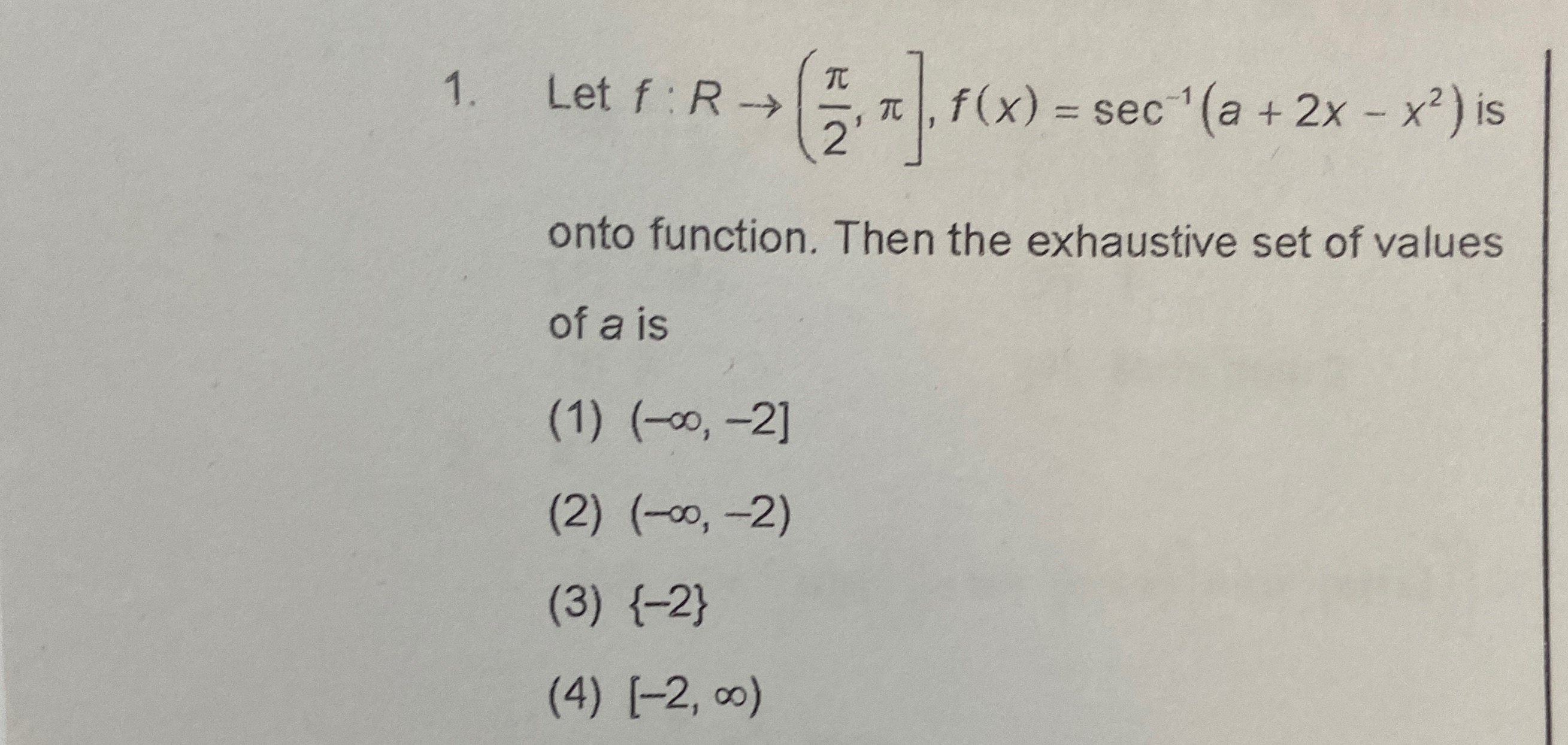
• A. $(-\infty, -2]$
• B. $(-\infty, -2)$
• C. $\{-2\}$
• D. $[-2, \infty)$

Answer 1

Answer: (C)

{-2}

Answer 2

The function is given by $f(x) = \sec^{-1}(a+2x-x^2)$. For $f(x)$ to be defined for all $x \in R$, the range of $g(x) = a+2x-x^2$ must be a subset of the domain of $\sec^{-1}$.

The domain of $\sec^{-1}y$ is $(-\infty, -1] \cup [1, \infty)$.

Let $g(x) = a+2x-x^2 = -(x^2-2x) + a = -(x-1)^2 + 1 + a$. The range of $g(x)$ for $x \in R$ is $(-\infty, a+1]$. So, we must have $(-\infty, a+1] \subseteq (-\infty, -1] \cup [1, \infty)$. This implies $a \le -2$.

Now, the function $f$ is onto the codomain $(\frac{\pi}{2}, \pi]$. This means that for every $y \in (\frac{\pi}{2}, \pi]$, there exists at least one $x \in R$ such that $f(x) = y$.

$y = \sec^{-1}(a+2x-x^2)$. Since $y \in (\frac{\pi}{2}, \pi]$, $\sec(y)$ is defined and $\sec(y) \in (-\infty, -1]$. Let $z = \sec(y)$. As $y$ ranges over $(\frac{\pi}{2}, \pi]$, $z$ ranges over $(-\infty, -1]$. So, for every $z \in (-\infty, -1]$, there must exist an $x \in R$ such that $a+2x-x^2 = z$. This means that the range of $g(x) = a+2x-x^2$ must include the entire interval $(-\infty, -1]$. The range of $g(x)$ is $(-\infty, a+1]$. So, we require $(-\infty, -1] \subseteq (-\infty, a+1]$. This inequality of intervals holds if and only if $-1 \le a+1$, which means $a \ge -2$.

For the function to be onto, both conditions must be met:

1. The range of $g(x)$ is a subset of the domain of $\sec^{-1}$. This gives $a \le -2$.
2. The range of $f(x)$ is equal to the codomain $(\frac{\pi}{2}, \pi]$. This means that the range of $g(x)$ must cover the values in the domain of $\sec^{-1}$ that map to $(\frac{\pi}{2}, \pi]$. The domain of $\sec^{-1}$ that maps to $(\frac{\pi}{2}, \pi]$ is $(-\infty, -1]$. So the range of $g(x)$ must be exactly $(-\infty, -1]$.

The range of $g(x) = a+2x-x^2$ is $(-\infty, a+1]$. For this range to be equal to $(-\infty, -1]$, we must have $a+1 = -1$. Solving for $a$, we get $a = -2$.

Thus, $a=-2$ is the only value for which the function is onto the given codomain.